题目背景

ICPC2020 WF E

题目描述

Interactive Creative Players Collective (ICPC) is working on a new computer game for which they want to generate realistic landscapes. One of the ICPC engineers proposed an algorithm inspired by geological processes. The algorithm starts with a flat landscape and repeatedly modifies it by lifting or lowering continuous blocks, thus forming horsts (lifted blocks) and grabens (lowered blocks). The blocks to be lifted or lowered are selected at random. ICPC hopes to obtain realistic landscapes this way.

Your task is to interpret any sequence of such modifications and output the resulting landscape. The landscape is represented by a sequence of $n$ integer height values, one for each integer point from $1$ to $n$ on the $x$-axis. Figure E.1 illustrates an example by connecting the height values with line segments.

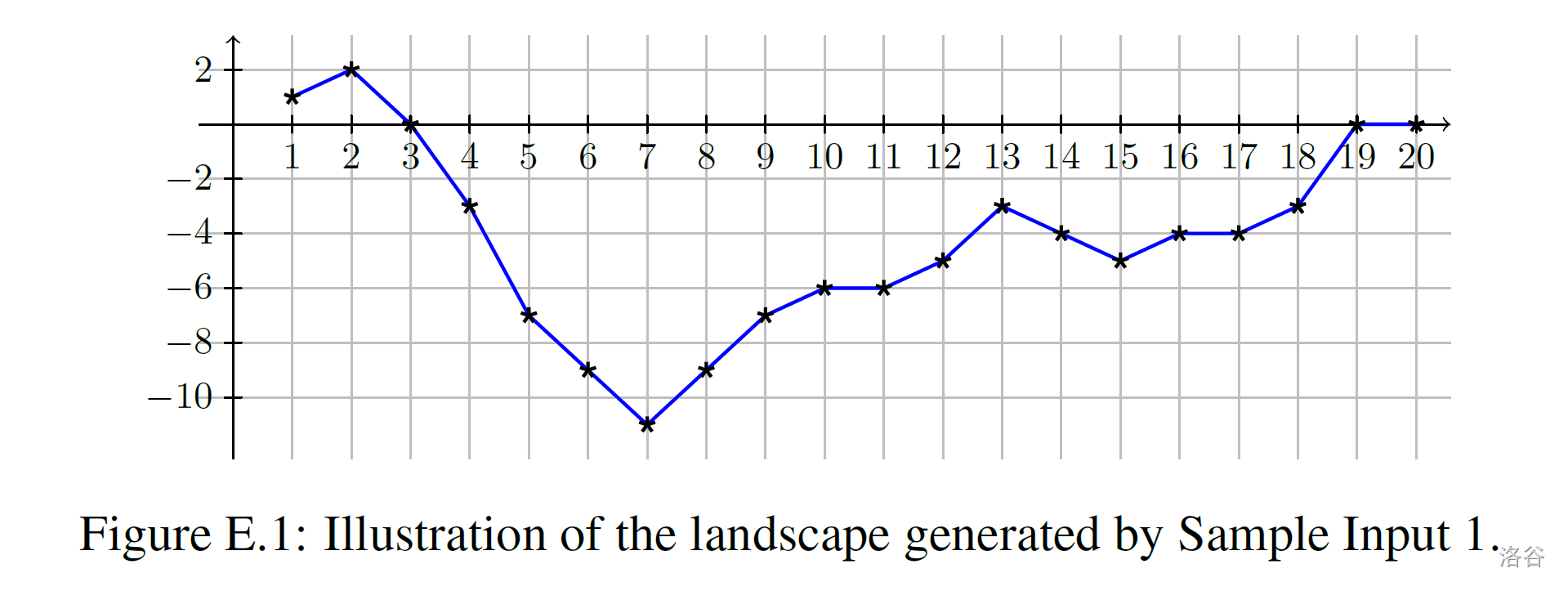
Initially the height is $0$ at all $n$ points. This flat shape is subjected to a sequence of modifications. Each modification applies one of the following four operations with two integer parameters $x_1 \leq x_2$:

• $\texttt{R}$: Raise -- increase the height by $1$ at all points between $x_1$ and $x_2$ inclusive.
• $\texttt{D}$: Depress -- decrease the height by $1$ at all points between $x_1$ and $x_2$ inclusive.
• $\texttt{H}$: Hill -- add a new linearly shaped hill between $x_1$ and $x_2$.
• $\texttt{V}$: Valley -- add a new linearly shaped valley between $x_1$ and $x_2$.

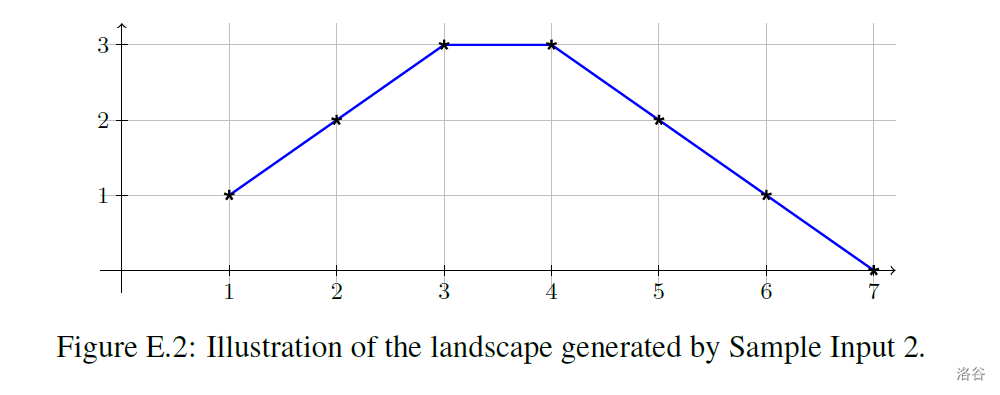
Adding a hill to the current landscape works as follows. The heights at points $x_1$ and $x_2$ are increased by $1$. If $x_2 - x_1 > 1$, the heights at points $x_1 + 1$ and $x_2 - 1$ are increased by $2$. If $x_2 - x_1 > 3$, the heights at points $x_1 + 2$ and $x_2 - 2$ are increased by $3$, and so on. Figure E.2 shows an example. Adding a valley works in the same way except the heights are decreased instead. The maximal change of height happens in the middle between $x_1$ and $x_2$. If $x_2 - x_1$ is odd, there will be two neighboring points with maximal change, otherwise just one.

输入格式

The first line of input contains two integers $n$ and $k$, where $n$ ($1 \leq n \leq 200\,000$) is the number of points, and $k$ ($0 \leq k \leq 200\,000$) is the number of modifications. The $n$ points along the $x$-axis are numbered from $1$ to $n$. The next $k$ lines describe the modifications. Each line contains one character $c$ and two integers $x_1$ and $x_2$, where $c$ (one of $\texttt{R}$, $\texttt{D}$, $\texttt{H}$ or $\texttt{V}$) designates the operation and $x_1$ and $x_2$ ($1 \leq x_1 \leq x_2 \leq n$) specify its parameters.

输出格式

Output $n$ lines, where the $i^{\text{th}}$ line contains the height at point $i$ after applying all modifications in the given order.

题目大意

题目背景

ICPC2020 WF E

题目描述

Interactive Creative Players Collective (ICPC)正在创作一款游戏，他们想为它生成真实的地形。一位ICPC工程师受地质过程启发，提出了一种算法，该算法从一个平地开始，重复地通过上升或下降一些连续的区块来改变地形，这样就会形成地垒（即上升的区块）和地堑（即下降的区块）。上升或下降的区块是随机选择的。ICPC希望通过这种方法获得真实的地形。

你的任务是根据所有的更改地形指令输出得到的地形，地形可表示为一个由$n$个整数组成的数组，每个整数代表$x$轴上的点$1$到$n$的海拔高度值。图表E.1是将这些值用折线连接起来的一个例子。

最初，这$n$个点的海拔都是0，接下来这个图形会受到一系列的修改，每条修改指令是以下四条之一，并且有两个参数$x_1 \le x_2$ ：

• $\texttt{R}$: Raise（上升）——将$x_1$到$x_2$的所有点的海拔均增加$1$。
• $\texttt{D}$: Depress（下降）——将$x_1$到$x_2$的所有点的海拔均减少$1$。
• $\texttt{H}$: Hill（山丘）——在$x_1$到$x_2$之间形成一座“山丘”。
• $\texttt{V}$: Valley（峡谷）——在$x_1$到$x_2$之间形成一条“峡谷”。

向现有地形添加一座“山丘”的原理如下：点$x_1$和$x_2$的海拔增加1；如果$x_2-x_1>1$，那么点$x_1+1$和$x_2-1$的海拔增加2；如果$x_2-x_1>3$，那么点$x_1+2$和$x_2-2$的海拔增加3；以此类推。图表E.2是一个例子。添加一条“峡谷”与上述原理相同，只是海拔是减少而非增加。海拔改变最大的点在$x_1$和$x_2$的中间，如果$x_2-x_1$是偶数，就会有两个相邻的点海拔改变最大，否则只有一个点。

输入格式

输入的第一行包含两个整数$n$和$k$，其中$n$ ($1 \le n \le 2\times10^5$)代表点的数量，$k$ ($0 \le k \le 2\times10^5$)代表修改指令的数量。$x$轴上的$n$个点被编号为$1$到$n$。

接下来的$k$行描述修改。每行包含一个字符$c$和两个整数$x_1$和$x_2$，其中$c$ (为$\texttt{R}$, $\texttt{D}$, $\texttt{H}$, $\texttt{V}$之一)代表操作种类，$x_1$和$x_2$ ($1 \le x_1 \le x_2 \le n$)是具体参数。

输出格式

输出共$n$行，其中第$i$行为所有修改完成后点$i$的海拔。

20 13
H 12 13
D 5 18
R 13 14
R 8 16
H 2 3
V 10 19
V 3 13
R 8 13
V 3 10
D 5 18
V 11 12
R 1 6
R 14 19

1
2
0
-3
-7
-9
-11
-9
-7
-6
-6
-5
-3
-4
-5
-4
-4
-3
0
0

7 1
H 1 6

1
2
3
3
2
1
0