#P7895. 『JROI-3』删树
『JROI-3』删树
题目背景
本题数据已加强,建议场上过了的同学再次提交确定做法正确性。
千万不要看错题!
——command_block 《考前小贴士》
你在 2021 年在洛谷打了一场比赛叫做 EZEC Round 6,其中里面有一道造树题你觉得特别水,随手就切了它。(所以没做过链接里题的人快来做啊!!!)
现在你在打 JROI-3 的月赛,你觉得造树太水了想删掉树,于是良心的出题人给了你一个机会。但是,在删除树之前,djy 想先知道树的边权和。
题目描述
这是一道交互题。
有一个 个节点的带边权的树,编号为 。每个点的度数是已知的。djy 想知道树上所有边的权值和,但他太菜了,不会去算如此简单的问题,因此把这个题扔给了您。
由于您很强,所以您可以对这棵树进行一些改变:删除所有度数为 的节点,得到剩下点的个数和每个点的度数。
您可以向交互库进行三种类型的提问:
- 对于当前树上存在的一个点,询问它的 dfs 序。
- 对于当前树上存在的一对节点,询问它们之间的距离。
- 删除当前树上所有度数为 的节点,同时删除与这些节点相邻的边,并且将所有未被删除的节点进行重新编号。保证剩下的节点的编号分别为 ,其中 是剩下的节点个数。
你需要操作不超过 142 次(包括提交答案),并在树删空之前求出当前树上所有边的权值和。
注:
- dfs 序:dfs 序指从当前的 号节点进行 深度优先搜索 ,每个节点被第一次访问的顺序。一棵树的 dfs 序不唯一。每次删除操作后 dfs 序会被重置。保证 dfs 序不随着其他操作而改变,即两次询问同一节点的 dfs 序的询问中间如果没有删除操作,保证回答相同的值。
- 距离:指在树上两点路径上的边权和。特别地,两个相同节点的距离为 。
输入格式
「交互模式」
本题采用 IO 交互模式。
在开始交互前,您需要先读入 ,表示树中点的个数。
接下来一行 个数,表示每个点的度数。
您可以进行三种类型的询问:
-
dfn u: 询问交互库编号为 的节点的 dfs 序。交互库返回一行一个整数,表示 的 dfs 序。 -
dis u v: 询问交互库编号为 和 的两个节点的距离。交互库返回一行一个整数,表示 和 的距离。 -
del: 要求交互库删除度数为 1 的点以及与之相连的边。交互库将对点进行重编号,并重新跑一个 dfs 序,交互库返回第一行一个整数为树的大小 ,第二行 个整数,第 个表示编号为 的点的度数。
如果您求出了当前树上所有边的边权和,按照 ! x 的格式输出答案 ,并立刻结束程序。
请保证作为询问参数的节点未被删除且 del 操作后树不为空。
如果您的操作不合法或次数大于 142 次,交互库会立刻终止程序,并将结果判定为 WA/RE/TLE/MLE。
在每一次询问之后,请不要忘记输出换行符以及清空缓存区,否则将会出现未知的错误。为了避免这种情况,您可以使用:
- 对于 C++,使用
fflush(stdout)或cout.flush()。 - 对于 Java,使用
System.out.flush()。 - 对于 Python,使用
stdout.flush()。 - 对于其他语言,请阅读相关文献。
输出格式
见 「交互模式」。
6
3 1 2 1 1 2
1
5
dfn 1
dis 6 2
! 17
提示
样例仅供理解交互过程,可能不符合逻辑。
【样例解释】
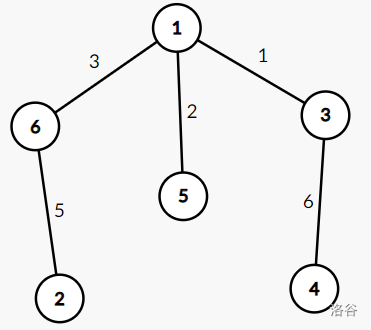
树的形态如上。
第一次询问节点 的 dfs 序,为 。
第二次询问节点 与节点 的距离,为 。
当前树上所有边的边权和为 。
【数据范围】
「本题采用捆绑测试」
- Subtask 1(1pts):。
- Subtask 2(4pts):。
- Subtask 3(20pts):。
- Subtask 4(10pts):树是一条链。
- Subtask 5(30pts):保证度数为 的点不超过 个。
- Subtask 6(20pts):。
- Subtask 7(15pts):无特殊限制。
对于 的数据,,每条边的边权不大于 且为正整数。
如果有假做法过了,请私信联系出题人加强数据。(如果有hack更好了)。
