题目背景
分割线下有形式化题面,可以配合食用。
题目描述
b6e0 有一棵树,树上第 i 个点有价值 ai。每条边长度为 1。
b6e0 会选择一个节点作为根节点。设这个节点为 r。然后,b6e0 会圈定一个节点的整个子树作为他的领地,设这个子树的根节点为 u。此时,树上的每个节点会给 b6e0 带来一些收益。在领地子树的根节点为 u 的情况下,节点 x 带来的收益 f(x,u) 定义如下:
- 当 x 在 u 的子树中时,它的收益为它父亲节点的收益加上它本身的价值 ax;
- 当 x 不在 u 的子树中时,它的收益为:与它相邻的节点中,与 u 距离(到 u 的简单路径长度)比 x 到 u 的距离远的节点,这些节点的收益对 998244353 取模的最大值,再乘上 ax。
在根节点为 r 的情况下,定义以 u 为子树的收益 W(u) 为所有节点的 f 值和。
当然,b6e0 有许多种选择根节点的方案。定义选 r 为根节点的收益 C(r) 为对于所有 u,以 u 为子树的收益(W(u))的和。对于每一个节点 r,求 C(r)。
形式化题面:
给你一棵有 n 个节点的树,第 i 个节点有点权 ai,每条边的长度为 1。当根节点为 r 时:
设 F(x) 表示 x 的父亲节点,特殊地,F(r)=0;D(x,y) 表示 x 到 y 的简单路径的长度,特殊地,对于所有 x,D(x,x)=0;Ax 表示 x 的子树中的节点(包括 x 本身)组成的集合,即 Ax={y∣D(x,y)=D(F(x),y)−1},特殊地,Ar={1,2,⋯,n};Bx 表示与 x 相邻的节点组成的集合,即 Bx={y∣D(x,y)=1}。
定义 f(x,u):
$$f(x,u)=\begin{cases}f(F(x),u)+a_x&x\in A_u\\a_x\cdot\max_{y\in B_x,D(y,u)>D(x,u)}\{f(y,u)\bmod 998244353\}&x\not\in A_u\end{cases}
$$
特殊地,对于所有 x,f(0,x)=0;在 x∈Au 的情况中,若对于所有 y∈Bx,都有 D(y,u)≤D(x,u),则 f(x,u)=ax。
定义节点 u 的分数 W(u)=∑v=1nf(v,u)。
定义节点 r 的收益 C(r) 表示以 r 为根时,∑i=1nW(i) 的值。
对于每一个节点 r,求 C(r)。
所有 C(r) 对 998244353 取模。
输入格式
第一行输入一个正整数 n 表示这棵树的节点数。
第二行输入 n 个整数,第 i 表示节点 i 的点权 ai。
下面 n−1 行,每行输入两个正整数 u,v,表示节点 u 与节点 v 之间有一条边。
输出格式
输出 n 行,第 i 行输出一个正整数表示节点 i 的收益 C(i) 对 998244353 取模的值。
6
7 2 5 100 1 5
1 3
3 4
1 2
4 5
4 6
67562
29930
75168
76888
63243
63283
提示
【样例解释】
样例中的树如下图:
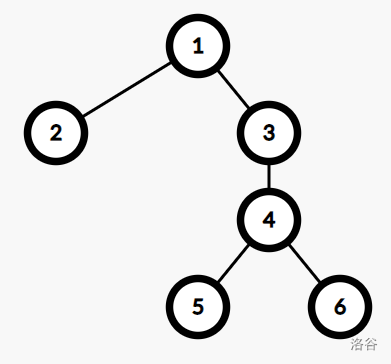
例如在 r=1,u=5 时,f(2,u)=a2=2,f(1,u)=a1⋅f(2,u)=14,f(3,u)=a3⋅f(1,u)=70,f(6,u)=a6=5,f(4,u)=a4⋅max{f(3,u),f(6,u)}=7000,f(5,u)=f(4,u)+a5=7001。
【数据范围】
- Subtask1(10pts):n≤200,ai≤103;
- Subtask2(20pts):n≤103;
- Subtask3(20pts):树为一条链;
- Subtask4(20pts):存在一个节点,使得它的度数为 n−1;
- Subtask5(30pts):无特殊限制。
对于 100% 的数据,1≤n≤5×105,1≤ai≤109。

