题目描述

译自 [CERC2018] Mirrority Report

在物理课上，每个学生都要完成一个半期作业。你选择做一个实验，探究一种稀有的不稳定粒子的性质，这种粒子名为红色粒子。一个红色粒子永远沿直线传播，直到它被镜子反射。

我们的实验可以看做一些单次反射镜组，这些反射镜可以看成二维平面上能够无限延伸的直线。一面单次反射镜只会在粒子第一次到达时将其反射，并且无论从什么方向入射都可以反射，但在此之后，粒子就只会穿过镜子了。

在反射时，遵循反射定律。如果粒子到达了两面反射镜的交点，这个粒子就会崩解，否则会进行反射。

镜子的摆放方式是你的实验老师设定的，你的任务是求出从一个点出发，有多少种出发的方向会让这个粒子到达一个特定的点。

输入格式

第一行一个整数包含一个非负整数 $N$，表示镜子的个数；

第二行包含四个整数 $S_x,S_y,E_x,E_y$，表示粒子从 $(S_x,S_y)$ 出发，终点是 $(E_x,E_y)$；

接下来 $N$ 行，每行四个整数 $A_x,A_y,B_x,B_y$，表示第 $i$ 面镜子上的两点。

所有输入的坐标值均在 $[-100,100]$ 之间。 起点和终点不同。从起点或终点到任何镜子的距离均不为零。

保证输入中不存在任何一组合法方案使得：粒子在任何可以反射该粒子的反射镜上的入射点到两面镜子的交点间的距离小于 $10^-$$^4$。

输出格式

输出一行一个整数，表示从 $(S_x,S_y)$ 出发，有多少种出发的方向会让这个粒子到达 $(E_x,E_y)$。

2
2 3 4 2
2 2 3 3
1 4 3 4

1

3
2 3 5 2
1 3 1 1
2 4 4 2
5 4 6 5

1

1
0 0 4 0
0 4 4 4

2

提示

样例 1 如下图：

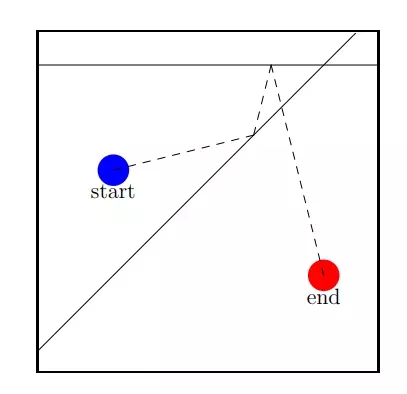
样例 2 如下图：

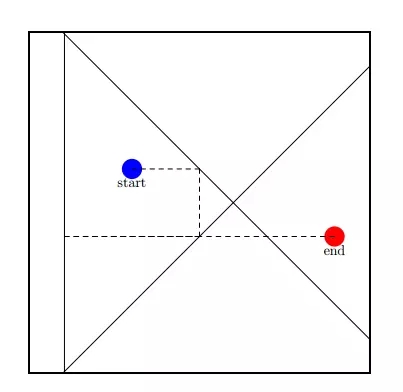
样例 3 如下图：

$0≤N≤8$