#P6738. [BalticOI 2014] Cop and Robber (Day1)
[BalticOI 2014] Cop and Robber (Day1)
题目背景
本题为交互题。
请使用 C++14/C++17 提交以避免不必要的 CE。
你需要将你的函数包裹在 extern "C" { } 中,具体的,一种包裹方式如下:
extern "C" {
const int N = 500;
int start(int n, bool a[N][N]) {
// ...
}
int nextMove(int x) {
// ...
}
}
题目描述
警察抓小偷,每名警察会选择一个街角进行把守,每次警察可以选择不动或者挪动到相邻的角落,小偷初始也在一个街角,因为他知道地图,所以他会选择最好的策略进行移动,但是小偷不能原地不动。
每一轮先是警察进行移动,然后是小偷进行移动,有下面两种结局:
- 小偷能够一直躲避警察
- 在一个街角上,小偷和警察相遇了,小偷被逮捕了
求警察能不能抓到小偷,能的话输出最小轮数。
您的代码必须以小偷一方为优胜策略方。
交互策略
你需要写两个函数与交互器进行交互,函数原型分别为:
int start(int N, bool A[MAX_N][MAX_N]);
int nextMove(int R);
-
其中
start(N, A)传入以下参数:-
——街角的数量(街角以 到 编号);
-
——一个二维数组描述小巷:对于所有的 ,若 与 不连通,则 ,否则
所有小巷都是双向的(即对于所有 和 ,),并且不会出现自环(即对于所有 ,)。此外,你可以假设警察总能从其他街角通过小巷到达一个街角。
-
如果警察可能在由参数描述的地图上抓到强盗,函数start应该返回警察与强盗相遇的街角编号。否则返回 。
- 而
nextMove(R)传入参数 ,表示当前强盗的所在的街角编号。该函数应返回这次移动之后警察所在的街角编号。
函数 start 必定会在第一次调用函数 nextMove 调用一次。如果 start 返回了 ,那么 nextMove 将不会被调用。否则,nextMove 会被反复调用直到追捕行动结束。更确切地说,只要满足以下情况之一,程序必须终止:
-
nextMove返回了一个不合法的移动; -
强盗能够一直躲避警察;
-
强盗被抓住了。
输入格式
None
输出格式
None
提示
样例说明
对于样例 ,图如下图所示:
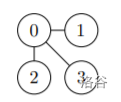
函数调用过程如下:
| 函数调用 | 函数返回 |
|---|---|
start(4, [[0, 1, 1, 1], [1, 0, 0, 0], [1, 0, 0, 0], [1, 0, 0, 0]]) |
3 |
nextMove(1) |
|
nextMove(0) |
0 |
数据规模与约定
本题采用捆绑测试。
- Subtask 1(16 pts):无重边。
- Subtask 2(14 pts):地图为网格形,如下:

- Subtask 3(30 pts):。
- Subtask 4(40 pts):。
对于 的数据,。
感谢交互库和 spj 作者
https://www.luogu.com.cn/user/60864
本题强制 优化。
