题目描述

Ysuperman 热爱在 TA 的幼儿园里散步，为了更方便散步， TA 把幼儿园抽象成 $n$ 个点，$m$ 条边的有向图。 散步得多了， TA 就给了每一条边无与伦比的亲密程度：$1,2,\cdots,m$，越大代表越亲密。 TA 也给了每一个点无与伦比的编号：$1,2,\cdots,n$，其中 $1$ 代表着幼儿园大门，但是每个点是没有亲密程度的。

接下来 $k$ 天，Ysuperman 每天会有一次散步计划。具体而言， TA 希望从 $x_i$ 号点出发，只经过亲密程度属于区间 $[l_i,r_i]$ 的边，走到幼儿园大门 $1$ 号点，期间经过的边的亲密程度必须单调递减，不然会因为 TA 有强迫症而不能回家。

Ysuperman 看着自己刚刚画的草稿脑子一团浆糊， TA 发现 TA 始终没有办法规划出这么多合理路线，现在 TA 想请你帮 TA 。具体而言，对于每一天的计划，如果可行，则输出 1，反之输出 0。

当然啦，有的时候 Ysuperman 很着急，需要你立马回复，有的时候 TA 可以等等你，先把所有问题问完再等你回复。

输入格式

第一行三个整数 $n,m,k,w$，分别表示节点个数、边个数、Ysuperman 的计划个数，和 Ysuperman 的焦急程度，此处的 $w$ 在后续输入中有用。

此后 $m$ 行的第 $i$ 行有两个整数 $u_i,v_i$，表示 Ysuperman 的幼儿园里有一条 $u_i$ 号点到 $v_i$ 号点的单向边，且亲密程度为 $i$。

此后 $k$ 行的第 $i$ 行有三个整数 $x_i,l_i,r_i$，表示 Ysuperman 的第 $i$ 个计划。

此处如果 $w=0$，则 $x_i,l_i,r_i$ 为明文，可以直接使用。

如果 $w=1$，则 $x_i,l_i,r_i$ 为密文，你需要将它解密。解密操作是：令 $L$ 为之前所有询问的输出之和（没有询问过则为 $0$），你需要将 $x_i ,l_i,r_i$ 都异或 $L$。

输出格式

$k$ 行，每行只可能是 1 或 0，第 $i$ 行的数表示第 $i$ 个计划是否可行。

5 7 5 0
3 2
1 2
4 3
5 4
3 1
5 3
5 1
3 1 4
1 2 2
5 5 6
4 5 7
2 1 7

0
1
1
0
0

5 12 10 0
4 2
4 2
5 3
3 3
1 5
1 4
4 4
2 4
5 3
1 5
2 2
4 1
4 3 5
4 2 3
1 4 5
3 1 8
3 1 4
3 5 5
2 1 12
4 10 12
2 5 5
1 1 3

0
0
1
0
0
0
0
1
0
1

5 12 10 1
4 2
4 2
5 3
3 3
1 5
1 4
4 4
2 4
5 3
1 5
2 2
4 1
4 3 5
4 2 3
1 4 5
2 0 9
2 0 5
2 4 4
3 0 13
5 11 13
0 7 7
3 3 1

0
0
1
0
0
0
0
1
0
1

提示

样例说明

样例说明 $1$

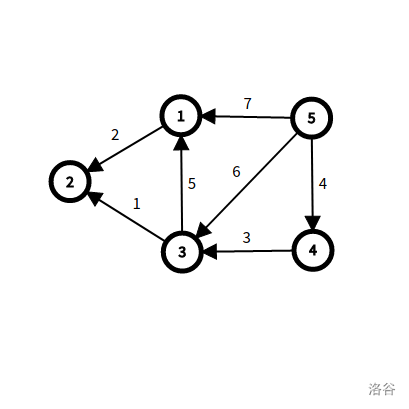
对于第 $2$ 条计划，Ysuperman 已经站在门口，所以计划可行。

对于第 $3$ 条计划，Ysuperman 只能通过路径 $5 \overset{6}{\rightarrow}3 \overset{5}{\rightarrow} 1$。（箭头上方数字表示的是边的亲密程度）。

其他计划都是不可行的。

样例说明 $3$

样例三为加密后的样例二。

---

数据范围

本题采用捆绑测试。

$\mathrm{subtask}$	$n$	$m$	$k$	特殊性质	分数
$1$	$\le17$		$\le 2\cdot 10^5$	/	$5$
$2$	$\le500$		$\le500$		$17$
$3$	$\le 3000$	$\le 3000$			$18$
$4$	$\le10^5$	$\le2\cdot10^5$		$v_i=1$	$13$
$5$	$\le 10^5$	$\le 2\cdot10^5$	$\le 10^5$	$l_i=1,w=0$	$7$
$6$	$\le10^5$	$\le2\cdot10^5$		$w=0$	$13$
$7$	$\le 10^5$	$\le 2\cdot10^5$		/	$27$

对于 $100\%$ 的数据，满足 $1 \le n \le 10^5 ,1 \le m \le 2\cdot10^5 ,0 \le k \le 2\cdot10^5$。

$w\in\{0,1\},1 \le u_i,v_i \le n$。

$x_i,l_i,r_i$ 在解密后保证 $1\le x \le n ,1 \le l_i,r_i \le m$。

提示

不保证不出现重边自环，不保证图联通。