题目描述

布里斯班被变异的袋熊占领，你必须带领大家去安全的地方。

布里斯班的道路像一个大网格，有 $R$ 条东西向的横向道路，从北向南依次编号为 $0,\cdots, (R - 1)$，有 $C$ 条南北向的纵向道路，从西向同东依次编号为 $0,\cdots, (C- 1)$ ，如下图所示。

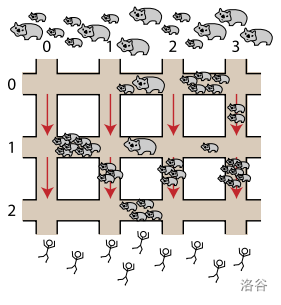
袋熊从北方入侵，人们逃向南方。人们可以在横向道路上双方向移动，但是在纵向道路上只能往南面安全的地方走。

横向道路 $P$ 和纵向道路 $Q$ 的交点表示为 $(P, Q)$ 。相邻 $2$ 个交点之间的道路线段上 有一些袋熊，且数目是随时间变化的。 你的任务是引导每个人从最北边（在横向道路 $0$ 上）的指定交点逃到最南端（在横向道路 $R - 1$ 上）的指定交点，路上经过 的袋熊最少。

首先会告诉你网格的规模以及每条道路线段上的袋熊的数量。然后给你一系列 $E$ 事件，每个事件是下列两者之一：

• 变化，表示有些道路线段上的袋熊数量发生变化；
• 逃离, 表示有些人已到达横向道路 $0$ 上指定交点，你必须给他们指出一条路，通往横向道路 $R - 1$ 上指定交点且路上遇到的袋熊最少。

举例

上图所示的初始地图中有 $3$ 条横向道路 （$R = 3$ ）和 $4$ 条纵向道路（$C = 4$ ），每 条道路线段上的袋熊数目如线段上的标记所示。考虑下列事件：

• 一个人到达交点 $A = (0, 2)$ ,希望逃到交点 $B = (2, 1)$ 。如图上虚线所示，他最少需要经过 $2$ 只袋熊。
• 又一个人到达交点 $X = (0, 3)$ ，希望逃到交点 $Y = (2, 3)$ 。如图上虚线所示，他最少需要经过 $7$ 只袋熊。
• 发生 $2$ 个变化事件：纵向道路 $0$ 上最上面那条道路线段上的袋熊数目变为 $5$，横向道路 $1$ 上中间那条道路线段上的袋熊数目变为 $6$，见下图中圈出来的两个数字。

• 第3个人到达交点 $A = (0, 2)$ ，希望逃到交点 $B = (2, 1)$ ，现在他最少需要经过 $5$ 只袋熊，如图中虚线所示。

输入格式

• 第 $1$ 行： $R$ 表示横向道路的数目，$C$ 表示纵向道路的数目。
• 第 $2$ 行： $H[0][0],\cdots,H[0][C-2]$。
• $\cdots$
• 第 $(R + 1)$ 行： $H[R-1][0],\cdots,H[R-1][C-2]$。
• 第 $(R + 2)$ 行： $V[0][0],\cdots,V[0][C-1]$。
• $H$: 二维数组 $R × (C - 1)$ ，其中 $H[P][Q]$ 表示交点 $(P, Q)$ 和交点 $(P, Q +1)$ 之间的横向道路线段上的袋熊数目。
• $\cdots$
• 第 $(2R)$ 行： $V[R-2][0],\cdots,V[R-2][C-1]$。
• $V$: 二维数组 $(R - 1) × C$ ，其中 $V[P][Q]$ 表示交点 $(P, Q)$ 和交点 $(P + 1,Q)$ 之间的纵向道路线段上的袋熊数目。
• 下一行: $E$。
• 下 $E$ 行：每行一个事件，按照事件发生的顺序给出。

如果 $C = 1$ ，表示横向道路上每条道路线段上的袋熊数目的若干空行(第 $2$ 到 $R +1$ 行)将会被省略。

表示每个事件的那一行格式如下：

• 1 P Q W 表示 将交点 $(P, Q)$ 和交点 $(P, Q + 1)$ 之间的横向道路线段上的袋熊数目改为 $W$。
• 2 P Q W 表示 将交点 $(P, Q)$ 和交点 $(P + 1, Q)$ 之间的纵向道路线段上的袋熊数目改为 $W$。
• 3 V1 V2 表示 计算一个人从交点 $(0, V1)$ 逃到交点 $(R-1, V2)$ 最少需要经过多少只袋熊。

例如：题目中的例子应该表示为以下格式

3 4
0 2 5
7 1 1
0 4 0
0 0 0 2
0 3 4 7
5
3 2 1
3 3 3
2 0 0 5
1 1 1 6
3 2 1

输出格式

对于每一次询问，给出最少经过袋熊数。

3 4
0 2 5
7 1 1
0 4 0
0 0 0 2
0 3 4 7
5
3 2 1
3 3 3
2 0 0 5
1 1 1 6
3 2 1

2
7
5

提示

对于 $100\%$ 的数据，$2 \le R \le 5 \times 10^3$，$1 \le C \le 200$，最多 $500$ 个变化，最多 $2 \times 10^5$ 次询问，任意时刻一条道路上最多 $10^3$ 只袋熊。