题目描述

天地之初，IOI 尚在遥远的梦想之中。

Serpent(水蛇) 生活的地方有 $N$ 个水坑，编号为 $0，\cdots，N - 1$，有 $M$ 条双向小路连接 这些水坑。每两个水坑之间至多有一条路径（路径包含一条或多条小路）相互连接，有些水坑之间根本无法互通(即 $M ≤ N-1$ )。Serpent 走过每条小路需要一个固定的天数，不同的小路需要的天数可能不同。

Serpent 的朋友袋鼠希望新修 $N - M - 1$ 条小路，让Serpent 可以在任何两个水坑间游走。袋鼠可以在任意两个水坑之间修路，Serpent 通过每条新路的时间都是 $L$ 天。

袋鼠希望找到一种修路方式使得修路之后 Serpent 在每两个水坑之间游走的最长时间最短。

举例说明

上图中有 $12$ 个水坑 $8$ 条小路 ($N = 12 , M = 8$)。假如 $L = 2$，即 Serpent 通过任何一条新路都需要 $2$ 天。那么，袋鼠可以修建 $3$ 条新路：

• 水坑 $1$ 和水坑 $2$ 之间；
• 水坑 $1$ 和水坑 $6$ 之间；
• 水坑 $4$ 和水坑 $10$ 之间。

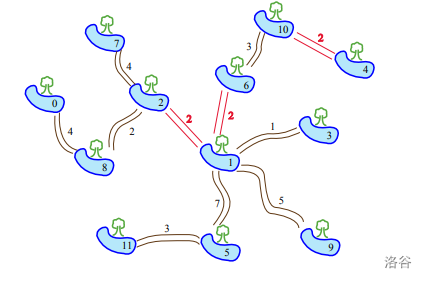
上图显示了修路后的最终状态。从水坑 $0$ 走到水坑 $11$ 的时间最长，需要 $18$ 天。这是最佳结果，无论袋鼠如何选择修路方式，总会存在一些水坑对，Serpent 需要 $18$ 天或者更长时间从其中一个走到另一个。

输入格式

• 第 $1$ 行: $N$ 表示水坑的数目，$M$ 表示原本存在的小路的数目，$L$ 表示 Serpent 通过新修的路径的时间。
• 第 $2,\cdots, M + 1$ 行: $A[i]$，$B[i]$，$T[i]$。$A$，$B$，$T$ 分别为三个包含 $M$ 个元素的数组，分别表示每条小路的两个端点和通过这条小路的时间。例如，第 $i$ 条小路连接水坑 $A[i-1]$ 和水坑 $B[i-1]$，通过这条小路的时间是 $T[i-1]$ 天。

例如：题目中的例子应该表示为以下格式

12 8 2
0 8 4
8 2 2
2 7 4
5 11 3
5 1 7
1 3 1
1 9 5
10 6 3

输出格式

如上所述，表示游走于两个距离最远的水坑之间所需的时间

12 8 2
0 8 4
8 2 2
2 7 4
5 11 3
5 1 7
1 3 1
1 9 5
10 6 3

18

提示

对于 $100\%$ 的数据，$1 \le N \le 10^5$，$0 \le M \le N-1$，$0 \le A[i],B[i] \le N-1$，$1 \le T[i] \le 10^4$，$1 \le L \le 10^4$。