题目背景

For the new year, Farmer John decided to give his cows a festive binary search tree (BST)!

To generate the BST, FJ starts with a permutation $a=\{a_1,a_2,\ldots,a_N\}$ of the integers $1\ldots N$, where $N\le 300$. He then runs the following pseudocode with arguments $1$ and $N.$

generate(l,r):
  if l > r, return empty subtree;
  x = argmin_{l <= i <= r} a_i; // index of min a_i in {a_l,...,a_r}
  return a BST with x as the root, 
    generate(l,x-1) as the left subtree,
    generate(x+1,r) as the right subtree;

For example, the permutation $\{3,2,5,1,4\}$ generates the following BST:

    4
   / \
  2   5
 / \ 
1   3

Let $d_i(a)$ denote the depth of node $i$ in the tree corresponding to $a,$ meaning the number of nodes on the path from $a_i$ to the root. In the above example, $d_4(a)=1, d_2(a)=d_5(a)=2,$ and $d_1(a)=d_3(a)=3.$

The number of inversions of $a$ is equal to the number of pairs of integers $(i,j)$ such that $1\le i<j\le N$ and $a_i>a_j.$ The cows know that the $a$ that FJ will use to generate the BST has exactly $K$ inversions $(0\le K\le \frac{N(N-1)}{2})$. Over all $a$ satisfying this condition, compute the remainder when $\sum_ad_i(a)$ is divided by $M$ for each $1\le i\le N.$

题目描述

为了迎接新年，Farmer John 决定给他的奶牛们一个节日二叉搜索树！

为了生成这个二叉搜索树，Farmer John 从一个 $1 \dots N$ 的排列 $a= \{1,2, \dots ,N\}$ 开始，然后以参数 $l$ 和 $r$ 开始运行如下的伪代码：

generate(l,r):
  if l > r, return empty subtree;
  x = argmin_{l <= i <= r} a_i; // index of min a_i in {a_l,...,a_r}
  return a BST with x as the root, 
    generate(l,x-1) as the left subtree,
    generate(x+1,r) as the right subtree;

例如，排列 $\{ 3,2,5,1,4 \}$ 将产生如下的二叉搜索树：

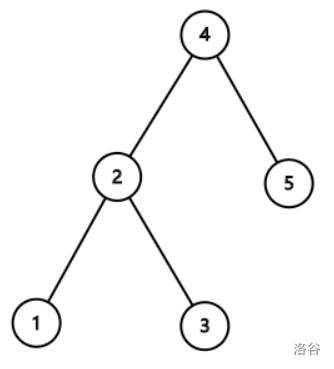
令 $d_i(a)$ 表示节点 $i$ 在用排列 $a$ 生成的二叉搜索树中的深度。深度定义为这个节点到根节点的路径上的点数。在上述例子中，$d_4(a)=1,d_2(a)=d_5(a)=2,d_1(a)=d_3(a)=3$。

$a$ 中的逆序对数等于满足 $1 \le i<j \le N$ 且 $a_i>a_j$ 的数对 $(i,j)$ 的个数。奶牛们知道 Farmer John 用来生成二叉搜索树的排列 $a$ 中恰好有 $K$ 个逆序对。对于所有满足条件的 $a$，请计算对于每个 $1 \le i \le N$，$\sum_a d_i(a)$ 对 $M$ 取模后的结果。

输入格式

输入只有一行，包含三个整数 $N,K,M$。

输出格式

输出一行 $N$ 个整数，第 $i$ 个整数表示 $\sum_a d_i(a) \bmod M$。两个整数之间用一个空格隔开。

3 0 192603497

1 2 3

3 1 144408983

3 4 4

提示

样例解释 1

对于这个样例，唯一满足条件的排列为 $a=\{1,2,3\}$。

样例解释 2

对于这个样例，满足条件的两个排列分别为 $a=\{1,3,2\}$ 和 $a=\{2,1,3\}$。

数据范围

对于全部数据，$1\le N\le 300$，$0\le K\le \frac{N(N-1)}{2}$，保证 $M$ 是一个 $\left[ 10^8,10^9+9 \right]$ 范围中的质数。

对于测试点 $3,4$，满足 $N \le 8$；

对于测试点 $5-7$，满足 $N \le 20$；

对于测试点 $8-10$，满足 $N \le 50$。

USACO 2019 December 铂金组T3