题目描述

在平面上，有 $n$ 个圆，记为 $c_1, c_2,...,c_n$ 。我们尝试对这些圆运行这个算法：

1. 找到这些圆中半径最大的。如果有多个半径最大的圆，选择编号最小的。记为 $c_i$。
2. 删除 $c_i$ 及与其有交集的所有圆。两个圆有交集当且仅当平面上存在一个点，这个点同时在这两个圆的圆周上或圆内。（原文直译：如果平面上存在一个点被这两个圆所包含，我们称这两个圆有交集。一个点被一个圆包含，当且仅当它位于圆内或圆周上。）
3. 重复上面两个步骤直到所有的圆都被删除。

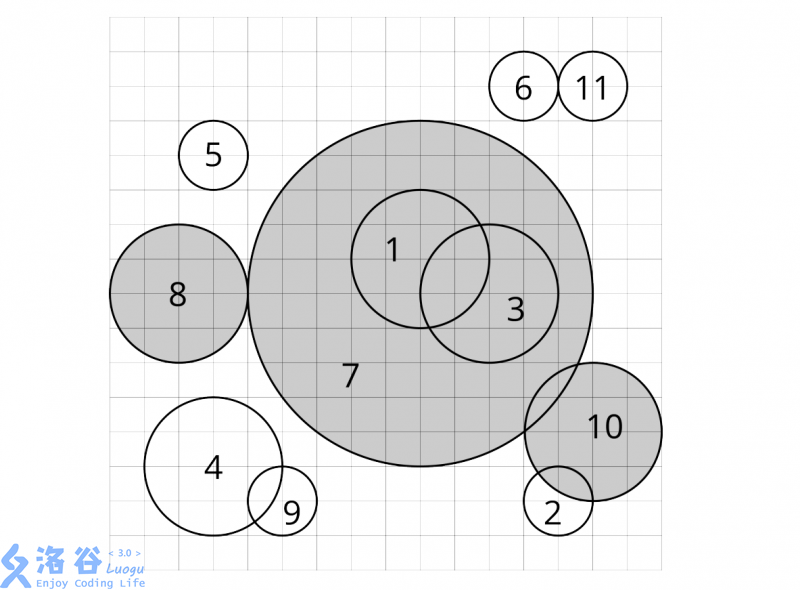
当 $c_i$ 被删除时，若循环中第 $1$ 步选择的圆是 $c_j$，我们说 $c_i$ 被 $c_j$ 删除。对于每个圆，求出它是被哪一个圆删除的。

输入格式

第一行包含一个整数 $n$，表示开始时平面上圆的数量。

接下来 $n$ 行，每行包含三个整数 $x_i, y_i, r_i$ 依次描述圆 $c_i$ 圆心的 $x$ 坐标、$y$ 坐标和它的半径。

输出格式

输出一行，包含 $n$ 个整数 $a_1, a_2, ..., a_n$，其中 $a_i$ 表示圆 $c_i$ 是被圆 $c_{a_i}$ 删除的。

11
9 9 2
13 2 1
11 8 2
3 3 2
3 12 1
12 14 1
9 8 5
2 8 2
5 2 1
14 4 2
14 14 1

7 2 7 4 5 6 7 7 4 7 6

提示

提示

题目描述中的图片对应了样例一中的情形。

子任务（注：这里给出的子任务与本题在这里的最终评测无关，仅供参考）

• Subtask 1(points: $7$): $n \leq 5000$
• Subtask 2(points: $12$): $n \leq 3 × 10^5$，对于所有的圆 $y_i = 0$
• Subtask 3(points: $15$): $n \leq 3 × 10^5$，每个圆最多和一个其他圆有交集
• Subtask 4(points: $23$): $n \leq 3 × 10^5$，所有的圆半径相同
• Subtask 5(points: $30$): $n \leq 10^5$
• Subtask 6(points: $13$): $n \leq 3 × 10^5$

所有数据均满足：$-10^9 ≤ x_i, y_i ≤ 10^9, 1 ≤ r_i ≤ 10^9$。