题目描述

小 R 和室友小 B 在寝室里玩游戏。他们一共玩了 n 局游戏，每局游戏的结果要么是小 R 获胜，要么是小 B 获胜。

第 1 局游戏小 R 获胜的概率是 $p_1$，小 B 获胜的概率是 1 − $p_1$。除了第一局游戏之外，每一局游戏小 R 获胜的概率与上一局游戏小 R 是否获胜有关。

具体来说：

1. 如果第 $i − 1$（$1 < i ≤ n$）局游戏小 R 获胜，那么第 $i$ 局游戏小 R 获胜的概率为 $p_i$，小 B 获胜的概率为 $1 − p_i$。

2. 如果第 $i − 1$（$1 < i ≤ n$）局游戏小 B 获胜，那么第 $i$ 局游戏小 R 获胜的概率为 $q_i$，小 B 获胜的概率为 $1 − q_i$。

小 D 时常过来看小 R 和小 B 玩游戏，因此他知道某几局游戏的结果。他想知道在他已知信息的条件下，小 R 在 $n$ 局游戏中总共获胜的局数的期望是多少。

小 D 记性不太好，有时他会回忆起某局游戏的结果，并把它加入到已知信息中；

有时他会忘记之前某局游戏结果，并把它从已知信息中删除。你的任务是：每当小 D 在已知信息中增加或删除一条信息时，根据小 D 记得的已知信息，帮助小 D 计算小 R 在 $n$ 局游戏中总共获胜局数的期望是多少。

需要注意的是：如果小 D 忘了一局游戏的结果，之后又重新记起，两次记忆中的游戏结果不一定是相同的。你不需要关心小 D 的记忆是否与实际情况相符，你只需要根据他的记忆计算相应的答案。

输入格式

第一行两个正整数 $n, m$ 和一个字符串 $\textrm{type}$。表示小 R 和小 B 一共玩了 $n$ 局游戏，

小 D 一共进行了 $m$ 次修改已知信息的操作，该数据的类型为 $\textrm{type}$。$\textrm{type}$ 字符串是为了能让大家更方便地获得部分分，你可能不需要用到这个输入，其具体含义见【限制与约定】。

接下来 $n$ 行，第 1 行包含一个实数 $p_1$，表示第一局比赛小 R 获胜的概率是 $p_1$。第 $i$（$1 < i ≤ n$）行包含两个实数 $p_i, q_i$。表示在第 $i − 1$ 局游戏小 R 获胜的情况下，第 $i$ 局游戏小 R 获胜的概率是 $p_i$；$q_i$ 表示在第 $i − 1$ 局游戏小 B 获胜的情况下，第 $i$ 局游戏小 R 获胜的概率是 $q_i$。

接下来 $m$ 行，每行描述一个小 D 已知信息的变化，操作分为两类。

1. add i c 表示小 D 回忆起了第 $i$ 局比赛的结果，并把它加入到已知信息中。若 $c = 0$ 表示第 $i$ 局比赛小 B 获胜，若 $c = 1$ 表示第 $i$ 局比赛小 R 获胜。数据保证 $i, c$ 均为整数且 $1 ≤ i ≤ n, 0 ≤ c ≤ 1$，如果这个操作不是第一个操作，保证在上一个操作结束后的已知信息中没有第 $i$ 局比赛的结果。

2. del i 表示小 D 忘记了第 $i$ 局比赛的结果，并把它从已知信息中删除。数据保证 $i$ 是整数且 $1 ≤ i ≤ n$，保证在上一个操作结束后的已知信息中有第 $i$ 局比赛的结果。

输出格式

对于每个操作，输出一行实数，表示操作结束后，在当前已知信息的条件下，小 R 在 $n$ 局游戏中总共获胜的局数的期望是多少。

3 3 A
0.3
0.5 0.2
0.9 0.8
add 1 1
add 3 0
del 1

2.350000
1.333333
0.432749

提示

【评分标准】

如果你的答案与正确答案的绝对误差在 $10^{-4}$ 以内，则被判定为正确。

如果你的所有答案均为正确，则得满分，否则得 $0$ 分。

请注意输出格式：每行输出一个答案，答案只能为一个实数。每行的长度不得超过 $50$。错误输出格式会被判定为 $0$ 分。

【限制与约定】

对于 $100\%$ 的数据，$1 ≤ n ≤ 200000$，$1 ≤ m ≤ 200000$，$0 < p_i, q_i < 1$。

对于 $100\%$ 的数据，输入保留最多四位小数。

本题共有 $20$ 个数据点，每个数据点 $5$ 分, 每个测试点的具体约定如下表：

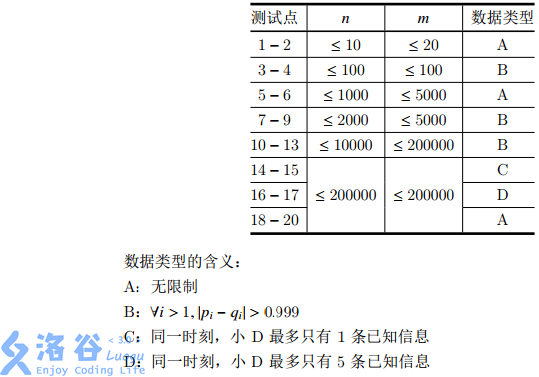
【小 R 教你学数学】

你可. 能. 会用到以下公式

1. 条件概率的计算方法

我们记 $p(A|B)$ 表示在已知事件 $B$ 发生时事件 $A$ 发生的概率，条件概率可以用以下公式计算：

$p(A|B)=\frac {p(AB)}{p(B)}$

其中 $p(AB)$ 表示事件 $B$ 和事件 $A$ 同时发生的概率，$p(B)$ 表示事件 $B$ 发生的概率。

2. 贝叶斯公式 (bayes)

由条件概率的计算方法，我们容易得到贝叶斯公式

$p(A|B)=\frac {p(B|A)p(A)}{p(B)}$

3. 全概率公式

如果随机变量 $x$ 有 $k$ 个取值，分别为 $x_1, x_2,\ldots , x_k$ 那么

$p(A)=\sum^{k}_{i=1} {p(A|x=x_i)p(x=x_i)}$

【温馨提示】

在本题中，如果你希望获得全部的分数，你可能需要考虑由于浮点数运算引入的误差。只使用加法和乘法运算不会引入太大的误差，但请谨慎使用减法和除法。

1. 两个大小相近的数相减可以引入非常大的相对误差。

2. 如果一个矩阵的行列式值非常小，那么求解该矩阵的逆可以带来相当大的误差。

当然，如果你的算法在数学上是正确的，但没有考虑浮点数运算的误差问题，可能仍然可以获得一部分的分数。