题目描述

自从上次神刀手帮助蚯蚓国增添了上千万人口（蚯口？），蚯蚓国发展得越来越繁荣了！最近，他们在地下发现了一些神奇的纸张，经过仔细研究，居然是 D 国 X 市的超级计算机设计图纸！

这台计算机叫做 “树状图”，由 $n$ 个计算节点与 $n - 1$ 条可以双向通信的网线连接而成，所有计算节点用不超过 $n$ 的正整数编号。顾名思义，这形成了一棵树的结构。

蚯蚓国王已在图纸上掌握了这棵树的完整信息，包括 $n$ 的值与 $n - 1$ 条网线的连接信息。于是蚯蚓国王决定，派出蚯蚓国最强大的两个黑客，小 P 和小 H，入侵 “树状图”，尽可能地摧毁它。

小 P 和小 H 精通世界上最好的编程语言，经过一番商量后，他们决定依次采取如 下的步骤：

• 小 P 选择某个计算节点，作为他入侵的起始点，并在该节点上添加一个 P 标记。
• 重复以下操作若干次（可以是 $0$ 次）：
  • 小 P 从他当前所在的计算节点出发，选择一条没有被标记过的网线，入侵到该网线的另一端的计算节点，并在路过的网线与目的计算节点上均添加一个 P 标记。
• 小 H 选择某个计算节点，作为她入侵的起始点，并在该节点上添加一个 H 标记。
• 重复以下操作若干次（可以是 $0$ 次）：
  • 小 H 从她当前所在的计算节点出发，选择一条没有被标记过的网线，入侵到该网线的另一端的计算节点，并在路过的网线与目的计算节点上均添加一个 H 标记。（注意，小 H 不能经过带有 P 标记的网线，但是可以经过带有 P 标记的计算节点）
• 删除所有被标记过的计算节点和网线。
• 对于剩下的每条网线，如果其一端或两端的计算节点在上一步被删除了，则也删除这条网线。

经过以上操作后，“树状图” 会被断开，剩下若干个（可能是 $0$ 个）连通块。为了达到摧毁的目的，蚯蚓国王希望，连通块的个数越多越好。于是他找到了你，希望你能帮他计算这个最多的个数。

小 P 和小 H 非常心急，在你计算方案之前，他们可能就已经算好了最优方案或最优方案的一部分。你能得到一个值 $x$：

• 若 $x = 0$，则说明小 P 和小 H 没有算好最优方案，你需要确定他们两个的入侵路线。
• 若 $x = 1$，则说明小 P 已经算好了某种两人合作的最优方案中，他的入侵路线。他将选择初始点 $p_0$，并沿着网线一路入侵到了目标点 $p_1$，并且他不会再沿着网线入侵；你只需要确定小 H 的入侵路线。
• 若 $x = 2$，则说明小 P 和小 H 算好了一种两人合作的最优方案，小 P 从点 $p_0$ 入侵到了 $p_1$ 并停下，小 H 从点 $h_0$ 入侵到了 $h_1$ 并停下。此时你不需要指挥他们入侵了，只需要计算最后两步删除计算节点与网线后，剩下的连通块个数即可。

输入格式

每个输入文件包含多个输入数据。输入文件的第一行为两个整数 $T$ 和 $x$，$T$ 表示该文件包含的输入数据个数，$x$ 的含义见上述。（同一个输入文件的所有数据的 x 都是相同的。）

接下来依次输入每个数据。

输出格式

对于每个数据，输出一行，表示在给定条件下，剩下连通块的最大个数。

1 0
13
1 2
2 3
2 4
4 5
4 6
4 7
7 8
7 9
9 10
10 11
10 12
12 13

8

8 0
1
2
1 2
3
1 2
2 3
4
1 3
2 3
2 4
5
1 5
2 5
3 5
4 5
16
1 2
1 3
1 4
1 5
5 6
5 7
5 8
5 9
9 10
9 11
9 12
9 13
13 14
13 15
13 16
17
1 2
1 3
1 4
1 5
5 6
5 7
5 8
5 17
17 9
9 10
9 11
9 12
9 13
13 14
13 15
13 16
17
8 6
2 6
11 6
4 6
14 2
10 2
5 4
1 4
9 8
17 11
12 5
3 6
13 6
16 8
7 11
15 16

0
1
2
2
4
12
13
10

8 1
1 1 1
2 1 1
1 2
3 2 2
1 2
2 3
4 2 2
1 3
2 3
2 4
5 5 5
1 5
2 5
3 5
4 5
16 1 5
1 2
1 3
1 4
1 5
5 6
5 7
5 8
5 9
9 10
9 11
9 12
9 13
13 14
13 15
13 16
17 1 5
1 2
1 3
1 4
1 5
5 6
5 7
5 8
5 17
17 9
9 10
9 11
9 12
9 13
13 14
13 15
13 16
17 2 4
8 6
2 6
11 6
4 6
14 2
10 2
5 4
1 4
9 8
17 11
12 5
3 6
13 6
16 8
7 11
15 16

0
1
2
2
4
12
13
10

提示

• 若 $x = 0$，则该行只有一个整数 $n$。
• 若 $x = 1$，则该行依次有三个整数 $n, p_0, p_1$。
• 若 $x = 2$，则该行依次有五个整数 $n, p_0, p_1, h_0, h_1$。

保证 $p_0, p_1, h_0, h_1$ 均为不超过 $n$ 的正整数。

每个数据接下来有 $n - 1$ 行，每行有两个不超过 $n$ 的正整数，表示这两个编号的计算节点之间有一条网线将其相连。保证输入的是一棵树。

同一行相邻的整数之间用恰好一个空格隔开。

数据文件可能较大，请避免使用过慢的输入输出方法。

【样例 1 说明】

这个输入文件只有一个输入数据。一种最优的方案如下：

• 小 P 从节点 $2$ 开始入侵，节点 $2$ 被小 P 标记。

• 小 P 从节点 $2$ 入侵到节点 $4$，节点 $4$ 和经过的网线被小 P 标记。

• 小 P 从节点 $4$ 入侵到节点 $7$，节点 $7$ 和经过的网线被小 P 标记。

• 小 H 从节点 $10$ 开始入侵，节点 $10$ 被小 H 标记。

• 删除被标记的节点 $2,4,7,10$ 和被标记的网线 $(2,4)$ 和 $(4,7)$。

• 删除任意一端在上一步被删除的网线。

此时还剩下 $8$ 个连通块。其中节点 $1,3,5,6,8,9,11$ 各自形成一个连通块，节点$12,13$形成了一个连通块。

【样例 2 说明】

• 数据 1：只有 $1$ 个计算节点，唯一可行的方案是小 P 从节点 $1$ 开始入侵（并马上停止），小 H 也从节点 $1$ 入侵到节点 $1$。所有的节点都被删去，剩下 $0$ 个连通块。

• 数据 2：一种最优方案是，小 P 从节点 $1$ 入侵到节点 $1$，小 H 也从节点 $1$ 入侵到节点 $1$。在删除操作后，剩下 $1$ 个连通块（只有节点 $2$）。

• 数据 3：唯一的最优方案是，小 P 从节点 $2$ 入侵到节点 $2$，小 H 也从节点 $2$ 入侵到节点 $2$，剩下 $2$ 个连通块。

• 数据 4：一种最优方案是，小 P 从节点 $2$ 入侵到节点 $2$，小 H 也从节点 $2$ 入侵到节点 $2$，剩下 $2$ 个连通块。

• 数据 5：唯一的最优方案是，小 P 从节点 $5$ 入侵到节点 $5$，小 H 也从节点 $5$ 入侵到节点 $5$，剩下 $4$ 个连通块。

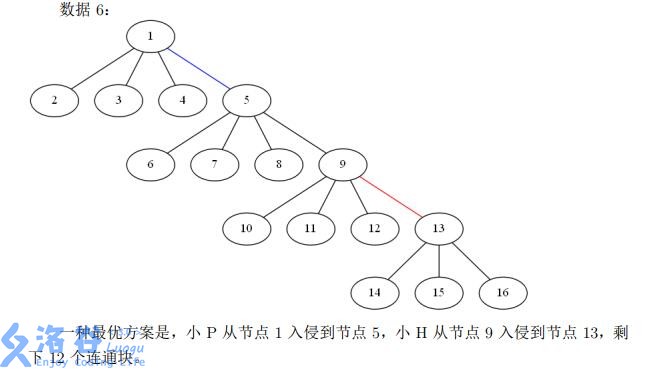
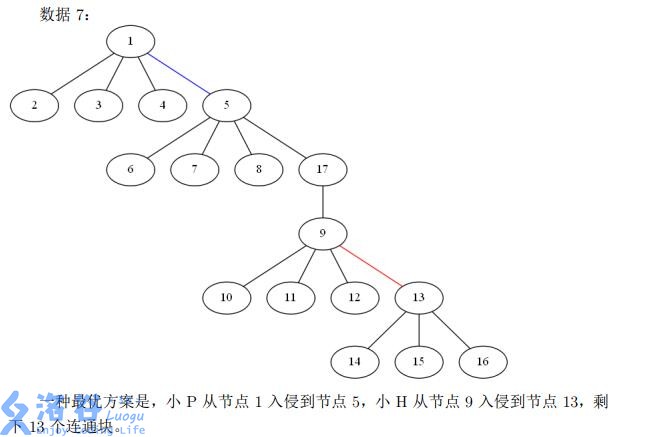
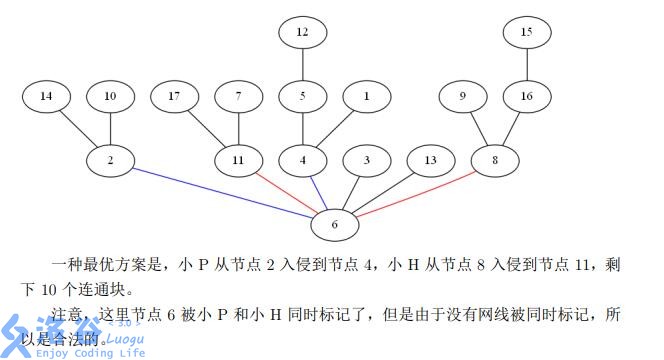
对于整数 $k$，设$\sum n^k$ 为某个输入文件中，其$T$ 个输入数据的 $n^k$ 之和。

对于所有数据，$T \leq 10^5, \sum n^1 <5 \times 10^5$

请注意初始化的时间复杂度，避免输入大量小数据时超时。

每个测试点的详细数据范围见下表。如果表中 “完全二叉” 为 Yes，则该输入文件的每个数据满足：网线信息的第 $j$ 行 $(1 \leq j < n)$ 输入的两个数依次是 $\left\lfloor \frac {j + 1} {2} \right\rfloor$ 和 $j + 1$。