题目描述

A triangular grid consists in equilateral triangles with side length 1 (see p. 3). A path in the triangular grid is an arbitrary finite sequence of triangles (with side length 1) of the grid such that every two successive ones share a side.

A shape formed by the points of any finite number of triangles is called an isle if any two triangles of the grid contained in this shape are connected by some path formed by the triangles contained in the shape.

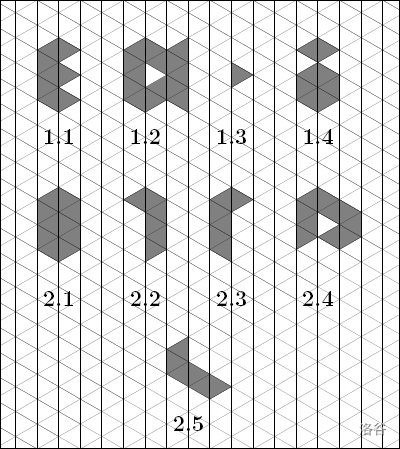
The shapes in the figures 1.1, 1.2 and 1.3 are isles.

The shape in the figure 1.4 is not an isle.

The shapes in the figures 2.2, 2.3 and 2.5 are congruent.

We aim at obtaining a systematic description, for each , of all non-congruent isles that can be formed by triangles with side length 1, and calculating how many such isles there are.

The boundary of every isle formed by at most ten triangles is a polygonal chain consisting of unitary segments of the grid. It can be revolved about, i.e.

it can be contoured without detaching pencil from the sheet, in such a way that its every segment is followed once, and we come back to the initial point. It may happen though that some point has to be crossed more than once (see Figure 2.4).

Luckily, in case of isles formed by at most ten triangles the shape's perimeter is connected (and can be thus contoured without detaching pencil from the sheet), unlike the one in Figure 1.2.

While circling around the perimeter, after each unit segment we make a turn of either of the following types:

a - 120 degrees left, b - 60 degrees left, c - 0 degrees (i.e. no turn, actually), d - 60 degrees right, e - 120 degrees right.

Each cycle around the isle can be described by a word consisting of letters from the set , where each letter tells which turn should be made after each successive unit segment the perimeter consists of. The cycle description has as many letters as there are such unit segments. This means we also describe the turn after the last segment of the polygonal chain, even though it is not required to uniquely determine the shape. This redundant letter is, however, very helpful in transforming one description of a cycle around the shape to another one that differs only in the initial point.

The words cdddcddd, dcdddcdd, cbbbcbbb describe different cycles around the shape of the Figure 2.1.

The words cbeddcde, adcabcbb, abcbbadc describe different cycles around the shape of the Figure 2.2.

The words acdabbcb i cddebced describe different cycles around the shape of the Figure 2.3.

If the inside of the shape is constantly on right hand side during a cycle around some shape, we call such cycle a clockwise cycle.

One can determine, for each isle, the set of all isles congruent with it and these isles' clockwise cycles.

The code of an isle is such a word that:

it is a description of a clockwise cycle around the contour of some isle congruent with the latter, it is the lexicographically smallest of all words satisfying the previous condition.

For the isle depicted in Figures 2.2 and 2.3, which are congruent, we take into account all clockwise cycles around each of them:

beddcdec, eddcdecb, ddcdecbe, dcdecbed, cdecbedd, decbeddc, ecbeddcd, cbeddcde and bcedcdde, cedcddeb, edcddebc, dcddebce, cddebced, ddebcedc, debcedcd, ebcedcdd so their common code is: bcedcdde, the lexicographically smallest of all the words above.

The code of the isle depicted in Figure 2.4 is: aadecddcddde.

Write a programme that:

for a given code of an isle of size generates the codes of all isles of size that can be obtained from the latter by adding one triangle to it, for a given integer generates the codes of all isles of size .

输入格式

In the first line of the standard input an integer (), denoting the number of queries, is given.

Each of the following lines contains a query of some type.

The query of type 1 consists of the letter K and a code of an isle formed by at most ten triangles, separated by a single space.

The query of type 2 consists of the letter N and an integer (), separated by a single space.

输出格式

The answers to the queries should be printed out to the standard output.

For queries of type 1 the number of distinct codes of isles that can be obtained by adding one triangle from isles congruent to the one described by the given code.

In the following line all these codes, separated by single spaces, should be printed in lexicographic order.

For queries of type 2 the number of distinct codes of isles formed by triangles should be printed.

In the following line all these codes should be printed in lexicographic order.

题目大意

三角形网格由侧长1的等边三角形组成（请参阅第3页）。三角形网格中的路径是三角形的任意有限序列（具有侧面长度1）的网格，使每两个连续的连续序列共享一个侧面。

如果任何有限数量的三角形的点形成的形状称为岛，则该形状中包含的两个三角形的形状与形状包含的三角形形成的某些路径连接。

图1.1、1.2和1.3中的形状是小岛。

图1.4中的形状不是小岛。

图2.2、2.3和2.5中的形状是一致的。

我们的目的是为每个非统一的小岛中的每个群岛获得一个系统的描述，该群岛可以由带有侧长1的三角形形成，并计算有多少此类小岛。

最多十个三角形形成的每个小岛的边界是由网格的单一段组成的多边形链。它可以旋转，即

它可以在不从纸上脱离铅笔的情况下进行轮廓，以使其每个部分都遵循一次，然后我们回到初始点。尽管必须将某个点越多一次，但可能会发生（见图2.4）。

幸运的是，与图1.2中的那个不同，如果最多是由十个三角形形成的小岛，则形状的周长是连接的（因此可以在不从纸上脱离铅笔的情况下轮廓）。

在周围盘旋时，每个单元段之后，我们进行以下两种类型的转弯：

A -120度左，B -60度左，C -0度（即实际上没有转弯），D -60度右，E -120度右侧。

岛周围的每个循环都可以通过一个由集合的字母组成的单词来描述，每个字母都告诉每个连续的单元段之后应进行哪个转弯。周期描述的字母与此类单元段一样多。这意味着我们还描述了多边形链最后一段之后的转弯，即使不需要唯一地确定形状。但是，这个冗余字母在将周围的一个周期的描述转换为仅在初始点上有所不同的一个周期的描述非常有帮助。

CDDDCDD，DCDDDCDD，CBBBCBBB一词描述了图2.1形状的不同周期。

cbeddcde，adcabcbb，abcbbadc词描述了图2.2形状的不同周期。

acdabbcb i cddebced词描述了图2.3形状的不同循环。

如果形状的内部在某个形状的周期中不断在右侧，我们将这种周期称为顺时针周期。

对于每个小岛，都可以确定与它一致的所有小岛的集合，这些小岛的顺时针循环。

小岛的代码是一个词：

这是对与后者一致的小岛轮廓周围顺时针周期的描述，它是满足先前情况的所有单词中最小的。

对于图2.2和2.3中描述的小岛，这是一致的，我们考虑了它们周围的所有顺时针周期：

beddcdec，eddcdecb，ddcdecbe，dcdecbed，cdecbedd，decbeddc，ecbeddcd，ceddcde和bcedcdde，cedcddeb，edcddebc，dcddebce，dcddebce上面的所有单词。

图2.4中描述的小岛的代码为：AADECDDCDDDE。

编写一个程序：

对于一个大小的给定代码，可以通过向其添加一个三角形来从后者获得所有大小的代码，对于给定的整数生成了所有大小岛的代码。

输出格式

查询的答案应将其打印到标准输出中。

对于类型1的查询，可以通过与给定代码描述的岛添加一个三角形来获得的不同小岛代码的数量。

在以下行中，应按词典顺序打印所有这些代码，分别为单个空间。

对于2型查询，应打印由三角形形成的群岛的不同代码的数量。

在以下行中，所有这些代码均应按词典形式打印。

2
K adeccecced
N 5

5
acedccecced addebcecced adebebecced adecbedcced cceccecce
4
aedddde bdecdde bececde ccedcde