题目背景
本题可能存在严重精度问题,部分数据下难以通过。本题数据较水,仅供参考。
题目描述
如题,给出一个 N 次函数,保证在范围 [l,r] 内存在一点 x,使得 [l,x] 上单调增,[x,r] 上单调减。试求出 x 的值。
输入格式
第一行一次包含一个正整数 N 和两个实数 l,r,含义如题目描述所示。
第二行包含 N+1 个实数,从高到低依次表示该 N 次函数各项的系数。
输出格式
输出为一行,包含一个实数,即为 x 的值。若你的答案满足以下二者之一,则算正确:
- 你的答案 x′ 与标准答案 x 的相对或绝对误差不超过 10−5。
- 你的答案 x′ 与标准答案 x 对应的函数值,即 f(x′) 和 f(x) 的相对或绝对误差不超过 10−5。
3 -0.9981 0.5
1 -3 -3 1
-0.41421
提示
对于 100% 的数据,6≤N≤13,函数系数均在 [−100,100] 内且至多 15 位小数,∣l∣,∣r∣≤10 且至多 15 位小数。l≤r。
【样例解释】
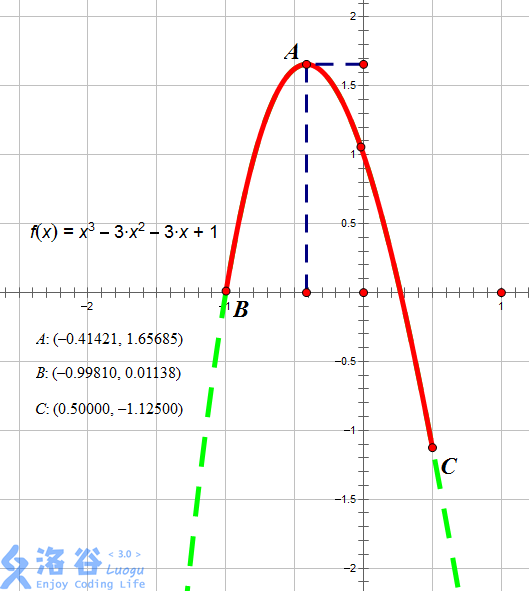
如图所示,红色段即为该函数 f(x)=x3−3x2−3x+1 在区间 [−0.9981,0.5] 上的图像。
当 x=−0.41421 时图像位于最高点,故此时函数在 [l,x] 上单调增,[x,r] 上单调减,故 x=−0.41421,输出 −0.41421。

