#P3305. [SDOI2013] 费用流
[SDOI2013] 费用流
题目描述
Alice 和 Bob 在图论课程上学习了最大流和最小费用最大流的相关知识。
最大流问题:给定一张有向图表示运输网络,一个源点 和一个汇点 ,每条边都有最大流量。
一个合法的网络流方案必须满足:
- 每条边的实际流量都不超过其最大流量且非负;
- 除了源点 和汇点 之外,对于其余所有点,都满足该点总流入流量等于该点总流出流量;而 点的净流出流量等于 点的净流入流量,这个值也即该网络流方案的总运输量。
最大流问题就是对于给定的运输网络,求总运输量最大的网络流方案。
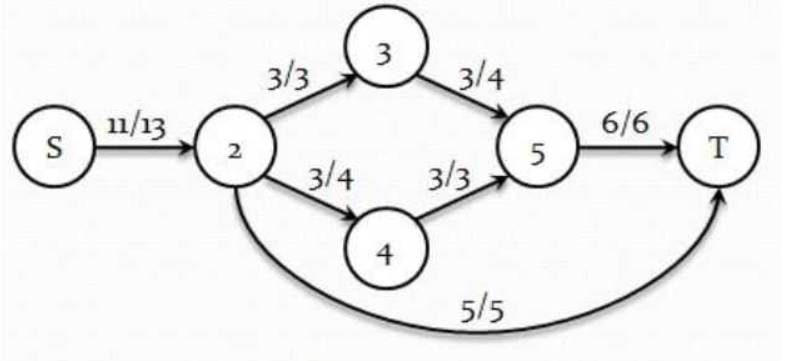
上图表示了一个最大流问题。对于每条边,右边的数代表该边的最大流量,左边的数代表在最优解中,该边的实际流量。需要注意到,一个最大流问题的解可能不是唯一的。
对于一张给定的运输网络,Alice 先确定一个最大流,如果有多种解,Alice 可以任选一种;之后 Bob 在每条边上分配单位花费(单位花费必须是非负实数),要求所有边的单位花费之和等于 。
总费用等于每一条边的实际流量乘以该边的单位花费。需要注意到,Bob 在分配单位花费之前,已经知道 Alice 所给出的最大流方案。现在 Alice 希望总费用尽量小,而 Bob 希望总费用尽量大。我们想知道,如果两个人都执行最优策略,最大流的值和总费用分别为多少。
输入格式
第一行三个整数 。 表示给定运输网络中节点的数量, 表示有向边的数量, 的含义见问题描述部分。为了简化问题,我们假设源点 是点 ,汇点 是点 。
接下来 行,每行三个整数 ,表示有一条从点 到点 的有向边,其最大流量是 。
输出格式
第一行一个整数,表示最大流的值。第二行一个实数,表示总费用。建议选手输出四位以上小数。
3 2 1
1 2 10
2 3 15
10
10.0000
提示
【样例说明】
对于 Alice,最大流的方案是固定的。两条边的实际流量都为 。
对于 Bob,给第一条边分配 的费用,第二条边分配 的费用。总费用为:。可以证明不存在总费用更大的分配方案。
【数据规模和约定】
对于 的测试数据,所有有向边的最大流量都是 。
对于 的测试数据,,。
对于 的测试数据:所有点的编号在 范围内,,,给定运输网络中不会有起点和终点相同的边。
