题目描述

近日，谷歌研发的围棋 AI——AlphaGo 以 $4:1$ 的比分战胜了曾经的世界冠军李世石，这是人工智能领域的又一里程碑。

与传统的搜索式 AI 不同，AlphaGo 使用了最近十分流行的卷积神经网络模型。在卷积神经网络模型中，棋盘上每一块特定大小的区域都被当做一个窗口。例如棋盘的大小为 $5\times 6$，窗口大小为 $2\times 4$，那么棋盘中共有 $12$ 个窗口。此外，模型中预先设定了一些模板，模板的大小与窗口的大小是一样的。

下图展现了一个 $5\times 6$ 的棋盘和两个 $2\times 4$ 的模板：

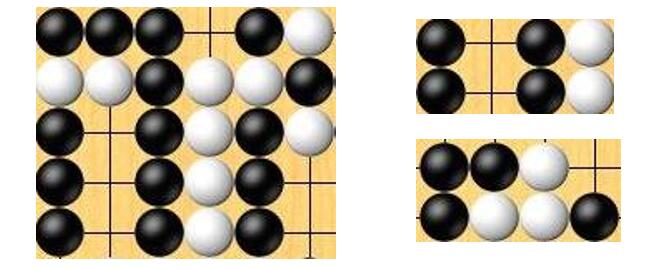
对于一个模板，只要棋盘中有某个窗口与其完全匹配，我们称这个模板是被激活的，否则称这个模板没有被激活。

例如图中第一个模板就是被激活的，而第二个模板就是没有被激活的。我们要研究的问题是：对于给定的模板，有多少个棋盘可以激活它。

为了简化问题，我们抛开所有围棋的基本规则，只考虑一个 $n\times m$ 的棋盘，每个位置只能是黑子、白子或无子三种情况，换句话说，这样的棋盘共有 $3^{n\times m}$ 种。此外，我们会给出 $q$ 个 $2\times c$ 的模板。

我们希望知道，对于每个模板，有多少种棋盘可以激活它。强调：模板一定是两行的。

输入格式

输入数据的第一行包含四个正整数 $n,m,c$ 和 $q$，分别表示棋盘的行数、列数、模板的列数和模板的数量。

随后 $2\times q$ 行，每连续两行描述一个模板。其中，每行包含 $c$ 个字符，字符一定是 W，B 或 X 中的一个，表示白子、黑子或无子三种情况的一种。

输出格式

输出应包含 $q$ 行，每行一个整数，表示符合要求的棋盘数量。由于答案可能很大，你只需要输出答案对 $10^9+7$ 取模后的结果即可。

3 1 1 2
B
W
B
B

6
5

提示

对于所有测试点：$1\leq n\leq 100$，$1\leq m\leq 12$，$1\leq c\leq 6$，$1\leq q\leq 5$。