题目背景

德国科学家总是对非洲野猴的抵抗力感到惊奇，因为他们发现在没有医疗条件的情况下，非洲野猴总是比其他所有野生动物少生病。最近的研究有了新发现，科学家 Dr.Smith 从非洲野猴身上发现了一种罕见的抗体，他猜测可能正是该罕见的抗体在帮助非洲野猴抵抗外来病毒的侵害。

Dr.Smith 就立刻展开了对该抗体的研究。在初始的观察中 Dr.Smith 发现该抗体没什么特别，而且非常简单，因为抗体的每组基因只有一对基元（Dr.Smith 把一组基因看成由若干对基元组成）。但是当 Dr.Smith 把病毒植入抗体所在的培养液后，奇迹出现了！那些简单的基因组通过不断地聚合（每个基因组两两合并生成新的基因组），最终所有的基因组合并成了一个非常庞大的基因组，而正是这庞大的基因组，因为聚合了所有原始基因组的优点，这庞大的基因组才可以慢慢地、逐个地去吃掉那些植入培养液的病毒。

下面是 Dr.Smith 在高倍显微镜下看到的抗体基因组基元聚合的大致过程：

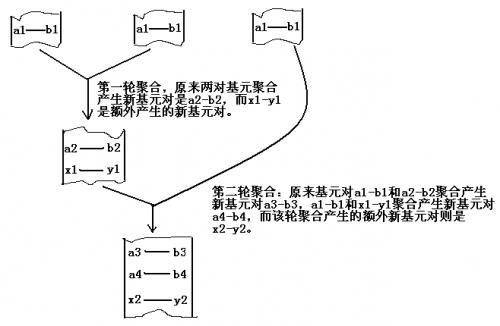
Dr.Smith 通过进一步观察和研究发现，抗体基因在聚合过程中似乎总是按照某个方法在进行，该方法能保证最终产生的基因组的基元对数量最多（每个基元对的存在能产生 $1$ 单位的生物能量），而在每次两个基因组聚合后所得到的新基因组的总的基元对由下面两部分相加组成：

1. 每两个基因组一发生聚合，就产生一个额外的、未知的基元对。
2. 当两个基因组聚合时，每个基因组中的每对基元都会与另一个基因组中的每对基元两两聚合产生一个新的基元对。

Dr.Smith 还发现，抗体在每个时刻总是只有两个基因组会发生聚合，也就是说，每两个基因组的聚合都是依次进行的，而不是同时进行的。

虽然观察到聚合原理，但 Dr.Smith 即使在知道一开始基因组个数的前提下，还是无法统计最终聚合产生的那个庞大的基因组所具有的总能量有多大。现在他想请你编程来统计一下。

题目描述

给定 $n$ 张写有数字 $1$ 的卡片和一台机器。

你需要进行以下操作 $n-1$ 次：将两张卡片放进机器并得到一张写有数字 $xy+1$ 的卡片，其中 $x,y$ 是放进去的两张卡片上所写的数字。

请问：进行 $n-1$ 次操作后，剩下的那张卡片上的数字最大会是多少？

输入格式

一行一个正整数 $n\ (1 \le n \le 10^4)$。

输出格式

一行一个正整数表示答案。

3

3