#P12920. [POI 2021/2022 R3] 河流 / Rzeki
[POI 2021/2022 R3] 河流 / Rzeki
题目背景
翻译来自于 LibreOJ。
题目描述
题目译自 XXIX Olimpiada Informatyczna – III etap Rzeki
等到最后一条河被污染,等到最后一棵树被砍掉,等到最后一条鱼被捕捉,然后我们才明白,原来钞票是不能吃的。——印第安谚语
在字节王国,有 条河流从南向北沿着直线 流动,还有 条河流从西向东沿着直线 流动。每两条河流的交点处都有一座城市。每座城市中,一条河流通过隧道流过,不与另一条混合。过去,每座城市都从其所在的河流取水。然而如今,一些河流污染严重,已无法净化水质,城市不得不从其他河流运水。运水成本等于城市到河流直线的距离。运水使用的是沿河流分布的双向公路,重卡可以通行(河流流向不影响运水)。
遗憾的是,字节王国的预算有限,可能无法为所有城市供水。更复杂的是,有些河流会被净化,有些又会重新污染。
请你编写一个程序,读取河流的当前状态,并支持两种操作:更改河流状态,以及回答在给定预算下最多能为多少城市供水。
输入格式
输入的第一行包含三个整数 ,分别表示南北向河流数、东西向河流数和操作次数。
第二行是一个长度为 的字符串,由 + 和 - 组成;第 个字符表示第 条南北向河流的状态:+ 表示干净,- 表示污染。第三行是一个长度为 的字符串,以相同格式描述东西向河流的初始状态。
接下来的 行描述操作,每行格式为以下之一:
- :询问在预算 下,最多能为多少城市供水;
- :第 条南北向河流状态改变(干净变为污染,或污染变为干净);
- :第 条东西向河流状态改变。
输出格式
对于每个 类型的询问,输出一行一个整数,表示在给定预算下最多能供水的城市数量。
3 4 11
--+
+++-
Z 1
M 1
M 2
M 3
Z 7
N 3
Z 1000000000000000000
M 2
N 2
Z 4
Z 1000000000000000000
11
9
0
10
12
提示
样例 1 解释
初始状态下,实线表示干净河流,虚线表示污染河流,共有 座城市位于交点处。
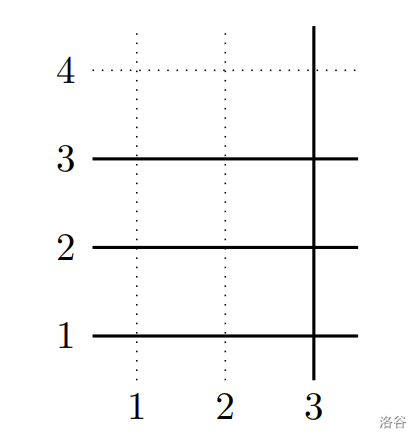
第一个询问 :城市 和 的运水成本为 ,因此只能放弃一座,其余 座成本为 ,故答案为 。
操作 、、 后,仅 座城市有直接干净河流。询问 :预算 可额外为 上的 座和 上的 座供水,总计 座。
附加样例
- 该样例满足 ,仅第 条南北向和东西向河流干净,询问预算 ;
- 该样例满足 ,每次询问时恰有一条干净河流(对 ,先净化第 条河流,询问成本 ,再污染第 条河流)。
详细子任务附加限制及分值如下表所示。
| 子任务编号 | 附加限制 | 分值 |
|---|---|---|
| 每条东西向河流始终污染 | ||
| 询问预算总和不超过 | ||
| 无附加限制 |
