题目背景

译自 Izborne Pripreme 2016 (Croatian IOI/CEOI Team Selection) D2T1。$\texttt{1s,0.5G}$。

「谁都无法相信未来，谁都无法接受未来。」

题目描述

给定一棵 $n$ 个点的二叉树，点有点权，其中 $1$ 号点为根节点。

$m$ 次操作修改某个点的点权。在每次修改后询问：这棵树上有多少个节点的子树（包含自身）是二叉搜索树（BST）？

我们给定 BST 的定义：

• 含有一个节点的树是 BST。
• 对于大于一个节点的树，它是 BST 当且仅当：
  • 根节点的左子树为空，或者左子树是二叉搜索树，且左子树内所有点的点权均不大于根节点的点权；
  • 根节点的右子树为空，或者右子树是二叉搜索树，且右子树内所有点的点权均不小于根节点的点权。

输入格式

第一行，两个正整数 $n,m$。

接下来 $n$ 行，每行两个整数 $l_i,r_i$，表示 $i$ 号点的左儿子和右儿子编号。

• 特别地，若不存在，则为 $0$。

接下来一行，$n$ 个整数 $a_1,\cdots,a_n$，表示每个点的点权。

接下来 $m$ 行，每行两个整数 $x,v$，表示一次操作 $a_x\gets v$。

输出格式

输出 $m$ 行 $m$ 个整数，表示答案。

6 5
2 3
4 0
5 6
0 0
0 0
0 0
4 1 3 2 2 5
3 3
2 2
3 5
5 4
6 1

4
5
5
6
4

8 10
4 5
8 0
0 0
3 7
0 6
0 0
2 0
0 0
7 0 9 3 6 0 6 2
3 0
4 0
8 2
2 3
7 6
1 6
5 7
6 9
1 1
1 7

3
3
3
6
6
6
6
8
7
8

提示

样例解释

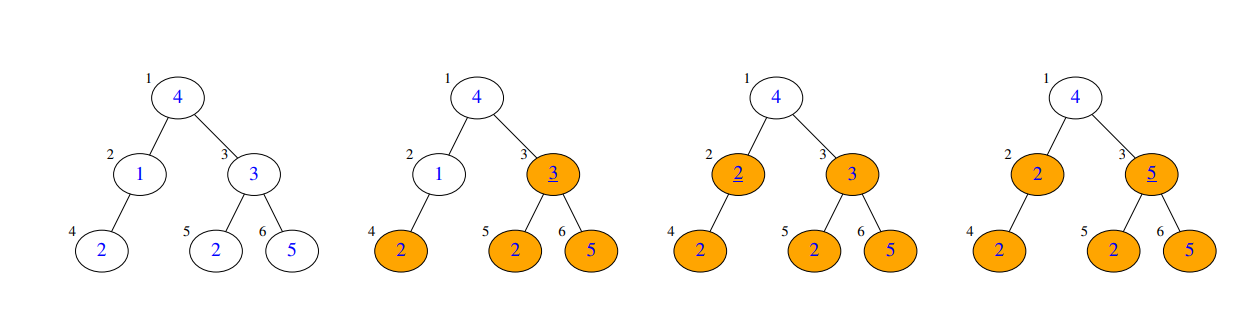
样例 $1$ 解释如图所示。

其中节点内的数字表示 BST 权值，节点外的数字表示节点编号。

数据范围

对于 $100\%$ 的数据，保证：

• $1\le n,m\le 2\times 10^5$；
• $0\le a_i,v\le 10^9$；
• 操作和树的形态均合法。

子任务编号	$n,m\le$	特殊性质	得分
$1$	$5\, 000$		$16$
$2$	$2\times 10^5$	A	$24$
$3$	$2\times 10^5$		$60$

特殊性质 A：$\forall 1\le i\le n$，$l_i=0\lor r_i=0$。