#P11191. 「KDOI-10」超级演出
「KDOI-10」超级演出
题目背景
本场比赛所有题目从标准输入读入数据,输出到标准输出。
题目描述
巡准备了一场超级演出。舞台和候场室可以看作一个包含 个点 条边的有向图,并且这个图当中没有环,也就是说,这是一张有向无环图(DAG)。
舞台为 号节点,保证所有节点均有到达节点 的路径。其余的节点均为候场室,每个候场室恰有一个剧团进行等待。
巡可以对一个候场室 发布出场命令:
- 如果这个候场室的剧团还没有出场,并且存在一条 的路径上没有其余候场的剧团。那么这个剧团就会沿着这条路径到达舞台进行演出,随后退场。注意:一个剧团退场后不会重新回到候场室。
- 否则,这个命令被认为是无效的。
巡有一个命令序列 和 次询问,每次给出一个区间 。巡想要知道如果依次对候场室 发布出场命令后,候场室还会剩下多少剧团等待演出。
注意:每次询问相互独立,也就是说,每次询问之前,每个候场室都恰有一个剧团进行等待。
输入格式
从标准输入读入数据。
输入的第一行包含一个正整数 ,表示测试点编号。 表示该测试点为样例。
第二行包含四个正整数 ,表示图的点数,边数,序列长度,和询问次数。
接下来 行,每行两个正整数 ,表示一条从 到 的有向边。保证无自环,无重边。
接下来的一行, 个正整数 。
接下来 行,每行两个正整数 ,表示一次询问的区间。
输出格式
输出到标准输出。
行,每行一个非负整数,表示一次询问的答案。
0
5 5 5 4
2 1
3 1
5 1
4 2
4 3
2 4 4 3 5
1 2
1 5
3 5
2 3
2
0
2
4
提示
【样例 1 解释】
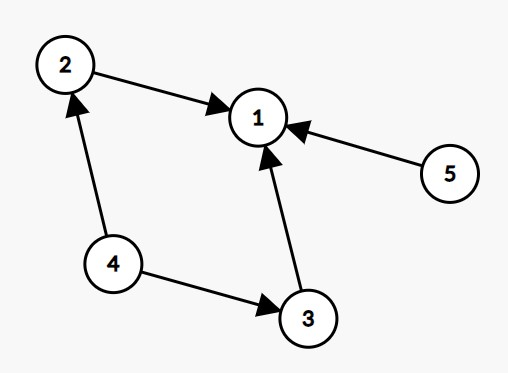
如图:
-
当询问 时:
- 发布出场命令 。 沿着 出场。
- 发布出场命令 。 沿着 出场。
此时余下 两个剧团,输出 。
-
当询问 时:
- 发布出场命令 。找不到 的且路上没有别的剧团的路线,该指令被认为无效。
- 发布出场命令 。找不到 的且路上没有别的剧团的路线,该指令被认为无效。
此时余下 四个剧团,输出 。
【样例 2】
见选手目录下的 show/show2.in 与 show/show2.ans。
这个样例满足测试点 的限制条件。
【样例 3】
见选手目录下的 show/show3.in 与 show/show3.ans。
这个样例满足测试点 的限制条件。
【样例 4】
见选手目录下的 show/show4.in 与 show/show4.ans。
这个样例满足测试点 的限制条件。
【样例 5】
见选手目录下的 show/show5.in 与 show/show5.ans。
这个样例满足测试点 的限制条件。
【样例 6】
见选手目录下的 show/show6.in 与 show/show6.ans。
这个样例满足测试点 的限制条件。
【数据范围】
对于全部的测试数据,保证:
- ;
- ;
- ,且不存在两组相同的 ;
- 对于任意 ,;
- 对于每组询问,;
- 输入构成一张有向无环图,且所有节点均存在到达节点 的路径。
| 测试点 | 特殊性质 | ||
|---|---|---|---|
| 无 | |||
| A | |||
| 无 | |||
| A | |||
| BC | |||
| C | |||
| BD | |||
| D | |||
| B | |||
| 无 |
- 特殊性质 A:图退化为一棵内向树,也就是说,除节点 外,每个点恰有一条出边,节点 没有出边;
- 特殊性质 B:保证对于每组询问,;
- 特殊性质 C:保证对于任意 ,;
- 特殊性质 D:保证每个点的入度和出度均不超过 。
