#P11159. 【MX-X6-T5】 再生
【MX-X6-T5】 再生
题目背景
原题链接:https://oier.team/problems/X6F。
このまま らったった 音に乗って 今きっと世界で僕だけだ 後ろ向きな歌を聴いて 少しだけ 前向きに生きていく
破碎的点依照破碎的规则进行重组,如此再生的一个结构将会是什么样的呢?
题目描述
现有一棵 个点的有标号有根树,给定其长链剖分得到的 top 数组,请你输出有多少种不同的树可以在长链剖分之后得到该 top 数组。答案对 (质数)取模。
具体来说,对于一棵树 ,对所有点 定义其树高 :
- 如果 是叶子,则 。
- 否则设 的孩子集合为 ,则 。
给定数组 ,你需要计算有多少种树满足:
- 对于根节点 ,满足 。
- 对于每一个不是叶子的节点 ,存在恰好一个孩子 满足 并且 ,其他孩子满足 。
模 (质数)。
两棵树不同当且仅当它们的根不同或它们的边集不同。
保证答案不为 ,但是不保证答案在模意义下不为 。
输入格式
第一行一个正整数 。
接下来一行, 个空格分隔的正整数 ,表示 top 数组。
输出格式
一行一个整数表示答案对 取模的值。
5
1 1 1 4 4
2
16
1 2 1 4 1 4 1 4 9 1 1 12 1 1 12 1
7181107
提示
【样例解释 #1】
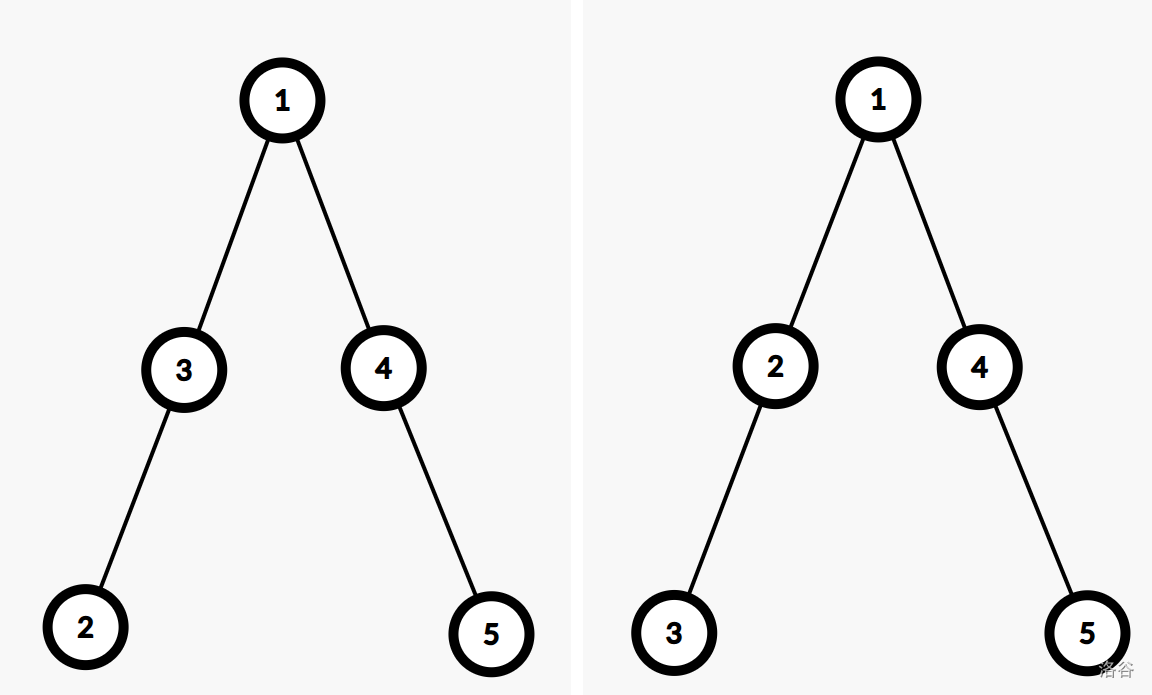
仅有图中的两种树满足条件。
【数据范围】
对于所有数据,保证 ,,保证取模前答案不为 。
捆绑测试,共 5 个 Subtask,具体限制如下所示:
- Subtask 1(11 pts):。
- Subtask 2(24 pts):。
- Subtask 3(17 pts):。
- Subtask 4(22 pts):。
- Subtask 5(26 pts):无特殊限制。
