#P11147. 「SFMOI Round I」Strange Dino Game
「SFMOI Round I」Strange Dino Game
题目背景
English statement. You must submit your code at the Chinese version of the statement.

Watersphere 同学在家没网了,只好玩起了 dino 游戏,但是他很菜,一玩到后面就头晕眼花,所以想让你编个程序帮助他拿到更高分,于是有了这题。
本题的游戏背景是 Dino。可以考虑点击链接游玩,以便更好理解题意。
题目描述
我们将问题放在二维平面上描述。我们给出一些游戏要素:
- 玩家:Dino。可以将其视为一个点。
- 障碍物:
- 仙人掌:形如 的线段。
- 飞鸟:形如 的线段。
- 游戏结束:Dino 与障碍物上的任意一点(包括线段端点)重合时,游戏结束。
- 起点:原点 。
- 终点:使游戏结束的位置,位于第一象限(或 轴上)。可能不存在(即游戏能无限进行)。
- 游戏分数:终点的 坐标。终点不存在时定义为无穷大。
- 跳跃参数:正整数 。
- 步行:Dino 在 轴上沿着 轴正方向移动。
- 跳跃:当 Dino 在 轴上时,可以进行一次跳跃。以起跳点为原点,跳跃轨迹为$$f(x) = \begin{cases}
\displaystyle \frac{h}{d}x & x\in [0, d) \\
\displaystyle-\frac{h}{d}x+2h & x\in [d, 2d) \\
\end{cases}$$
- 需要注意的是,由上述定义可以推出:在一次跳跃后落地的瞬间进行第二次跳跃是合法的。
- 需要注意的是,可以在任意实数点(只要在 轴上)处开始跳跃。也就是说,跳跃不一定在整点开始。
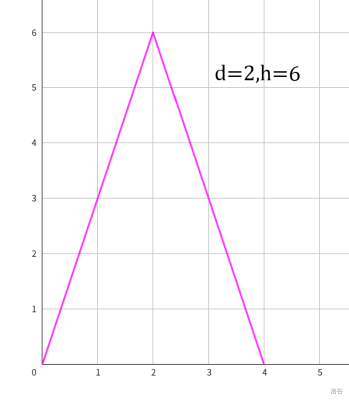
下图展示了 时的一次跳跃。
在一局游戏中,Dino 从起点出发向 轴正方向移动。目标是最大化得分,即尽量避开障碍物,使自己移动的距离尽量长。
每一时刻,Dino 只能做一件事:步行,或跳跃。当且仅当 Dino 在 轴上时可以进行跳跃。
形式化地说,Dino 的行为可以被描述为一个长度为 的实数二元组序列 ,满足:
- ;
- ;
- , ;
- ;(二段跳是不允许的)
- , 。
当 时,我们定义 Dino 在 进入步行状态,否则定义 Dino 在 进入跳跃状态。
当 Dino 与障碍物重合时,游戏结束。此时 Dino 在的位置为终点,得分为终点的 坐标。
已知有 只飞鸟和 个仙人掌,求出 Dino 的最大得分。特别地,得分可以为无穷大。
可参阅样例解释的图片。
输入格式
本题单个测试点内有多组测试数据。
第一行,一个正整数 ,代表游戏次数。
接下来依次描述 组数据:
- 每组数据第一行,两个正整数 ,表示 dino 的跳跃参数。
- 每组数据第二行,两个整数 ,表示飞鸟个数与仙人掌个数。
- 接下来 行,每行三个正整数 ,描述第 只飞鸟。
- 接下来 行,每行两个正整数 ,描述第 株仙人掌。
输出格式
对于每组数据输出一行,表示得分的最大值。
特别地,如果得分为正无穷,输出 Dino!。
2
1 3
1 2
1 2 1
2 2
3 2
1000000000 1000000000
1 0
114514 1919 810
3
Dino!
1
8 16
8 3
5 18 13
4 20 10
6 13 1
2 17 11
1 11 6
5 1 1
2 6 3
1 16 1
7 20
7 13
3 2
6
1
5 5
1 2
5 5 1
6 1
16 3
16
1
5 5
1 4
19 10 8
4 1
15 1
22 2
20 1
22
提示
样例 解释:
- 对于第 组数据,dino 无论如何也无法跳过连续的两株高为 的仙人掌,答案即为第二株仙人掌的 轴坐标。
- 对于第 组数据,dino 可以在原点直接起跳跳过唯一的一只鸟,也完全可以不起跳从飞鸟下方走过。
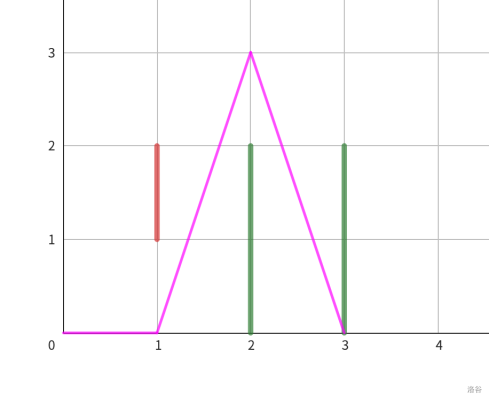
其中第一组数据的解释如下所示,红线代表飞鸟,绿线代表仙人掌,粉线代表 Dino 的轨迹。
数据范围
本题采用捆绑测试。
- Subtask 1(5 pts):;
- Subtask 2(5 pts):;
- Subtask 3(20 pts):;
- Subtask 4(20 pts):;
- Subtask 5(40 pts):无特殊限制。
- Subtask 6(10 pts):无特殊限制。
对于 的数据,保证:
- ;
- ;
- ;
- 。
