题目背景
原题链接:https://oier.team/problems/X5G。
Abiogenesis - Juggernaut.
本题为 Codeforces 1981 E. Turtle and Intersected Segments 改编。
题目描述
给 n 条线段 [li,ri],第 i 条线段有一组权值 ai,bi。
有一个无向图 G,其初始有 n 个结点,0 条边。对于每一对正整数 i,j 满足 1≤i<j≤n,若编号为 i,j 的线段相交,就在 G 中连一条两个端点分别为 i,j,边权为 ai+aj+∣bi−bj∣ 的边。
求 G 最小生成树边权之和,或报告 G 不连通。
如果两条线段 [l1,r1] 和 [l2,r2] 满足 max(l1,l2)≤min(r1,r2),就认为它们是相交的。
输入格式
本题有多组测试数据。
第一行输入一个正整数 T,表示测试数据组数。
对于每组测试数据:
第一行包含一个正整数 n,表示线段的个数。
之后的 n 行中的第 i 行包含四个正整数 li,ri,ai,bi。
输出格式
对于每组数据,输出一行一个整数,表示 G 最小生成树边权之和。特别地,若 G 不连通,输出 −1。
4
5
1 7 1 3
2 4 2 6
3 5 3 5
6 7 2 9
3 4 1 4
5
2 7 3 3
1 3 5 6
4 5 3 5
6 7 1 9
1 1 5 4
4
1 4 1 3
1 2 2 1
3 4 3 5
1 4 4 4
3
1 3 1 1
2 3 1 3
4 5 1 8
22
41
17
-1
提示
【样例解释】
对于第一组数据,G 的形态如下:
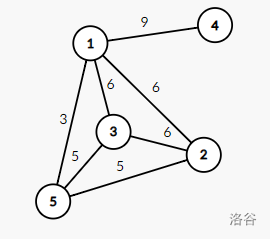
G 的其中一个最小生成树形态如下:
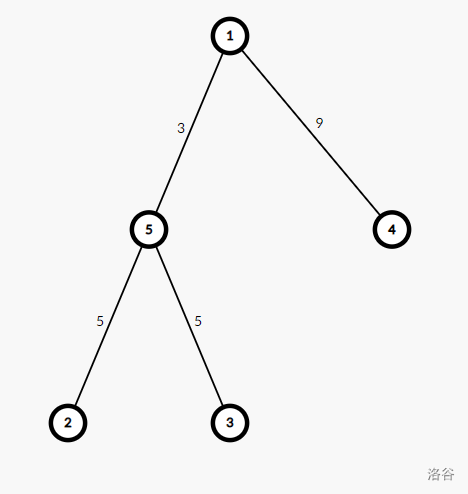
【数据范围】
本题采用捆绑测试且开启子任务依赖。
| 子任务编号 |
n≤ |
∑n≤ |
特殊性质 |
子任务依赖 |
分值 |
| 1 |
100 |
105 |
无 |
无 |
11 |
| 2 |
105 |
AC |
5 |
| 3 |
A |
2 |
14 |
| 4 |
B |
无 |
| 5 |
C |
2 |
| 6 |
D |
无 |
| 7 |
无 |
1,2,3,4,5,6 |
28 |
- 特殊性质 A:∀i∈[1,n],li=1。
- 特殊性质 B:$\forall i \in [1, n - 1], l_i \le l_{i + 1}, r_i \le r_{i + 1}$。
- 特殊性质 C:∀i∈[1,n],bi=1。
- 特殊性质 D:∀i∈[1,n],ai=bi。
对于所有数据,满足 1≤T≤104,1≤n,∑n≤105,1≤li,ri,ai,bi≤108,li≤ri。


