#P11127. [ROIR 2024] 二叉树的遍历 (Day 2)
[ROIR 2024] 二叉树的遍历 (Day 2)
题目背景
翻译自 ROIR 2024 D2T4。
二叉树有三种基本遍历方式:前序遍历(pre-order)、中序遍历(in-order)和后序遍历(post-order)。我们可以将这三种遍历方式进行概括:假设每个节点上记录一个整数 (取值范围为 到 ),表示在遍历中输出该节点的时机,具体如下:
- :在遍历其左右子树之前;
- :在遍历其左子树之后,遍历其右子树之前;
- :在遍历其左右子树之后。
因此,如果所有节点的 值都是 ,则遍历为前序遍历;如果都是 ,则为中序遍历;如果都是 ,则为后序遍历。
题目描述
考虑一棵有 个节点的二叉树,节点编号从 到 。树的根节点为 。最初,所有节点上的值都是 。
你需要处理 个操作,操作类型如下:
- 将节点 上的值更改为 ( 取值为 , 或 )。
- 查询节点 在当前遍历方式中的位置。
需要输出所有第二种类型的操作的结果。
输入格式
第一行包含两个整数 和 ()。
接下来 行,每行包含两个整数 和 (),分别表示节点 的左子树和右子树的编号,若某个子树不存在则为 。
保证 和 描述了一个有效的二叉树。
接下来的 行中包含操作。每行的第一个整数 ()表示操作类型。
- 对于第一种类型的操作,后面有三个整数 , 和 (, 为 , 或 ),表示节点范围和新的值。
- 对于第二种类型的操作,后面有一个整数 (),表示询问其在遍历中的位置的节点编号。
输出格式
对于每个第二种类型的操作,输出一个整数,表示对应节点在遍历中的位置。
5 5
3 4
0 0
5 2
0 0
0 0
2 2
1 1 3 1
2 5
1 3 3 0
2 3
4
1
2
提示
样例中的树是这样的:
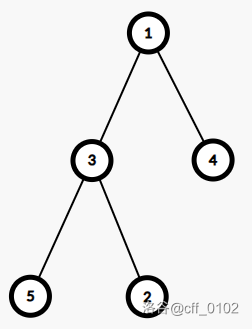
刚开始,所有节点的 值都是 ,因此第一次查询时遍历得到的数组为 , 在第四个位置。
在将节点 的遍历方式 改为 后,再次查询时遍历得到的数组为 , 在第一个位置。
接着把节点 的遍历方式 改为 ,此时再进行查询,遍历得到的数组为 , 在第二个位置。
设 为操作 的数量。
| 子任务 | 分值 | 特殊性质 |
|---|---|---|
| 同样例 | ||
| 所有操作一在所有操作二之前 | ||
| 所有叶子节点都与根节点距离相同,没有具有一个子节点的节点 | ||
| 对于所有操作一, | ||
| 对于所有操作一,,每个节点最多有一个子节点 | ||
| 对于所有操作一, | ||
| 每个节点最多有一个子节点 | ||
| 无 | ||
对于 的数据,。
