题目背景
翻译自 ROIR 2024 D1T4。
给定一棵由 n 个节点构成的树和一个数 k。固定树中的某个节点 s,并令其为根。
将树的边定向从树根出发。换句话说,将边 (u,v) 定向为 u→v,如果在以 s 为根时,节点 u 是节点 v 的父节点。在这种定向下,每个节点都可以从根到达。
定义节点 v 到节点 s 的距离为从 s 到 v 的最短路径上边的数量。定义节点 s 的可达性为所有节点到节点 s 的距离中的最大值。
题目描述
允许在树中增加不超过 k 条额外的有向边。对于树中的每个节点 s,确定如果选择节点 s 作为树根,能够达到的最小可达性是多少。
注意,在某些子任务中,只需要输出顶点编号为 1 的答案。
输入格式
第一行包含三个整数 n,k 和 t (2≤n≤2×105,1≤k≤n−1,n×k≤2×105,0≤t≤1),分别表示树的顶点数量、额外添加的有向边的最大数量限制和一个整数 t,如果 t 为 0,则只需输出顶点编号为 1 的答案;如果 t 为 1,则输出所有顶点的答案。
接下来的 n−1 行每行包含两个整数 ui 和 vi (1≤ui,vi≤n),表示树的一条边。
保证所给的边构成一棵树。
输出格式
如果 t=0,输出一个整数,即选择顶点编号为 1 作为树根,并且增加不超过 k 条额外的有向边时,可以达到的最小可达性。
如果 t=1,输出 n 个数,第 i 个数表示选择顶点 i 作为树根,并且增加不超过 k 条额外的有向边时,可以达到的最小可达性。
5 2 1
1 2
1 3
2 4
2 5
1 1 2 2 2
3 1 0
1 2
2 3
1
提示
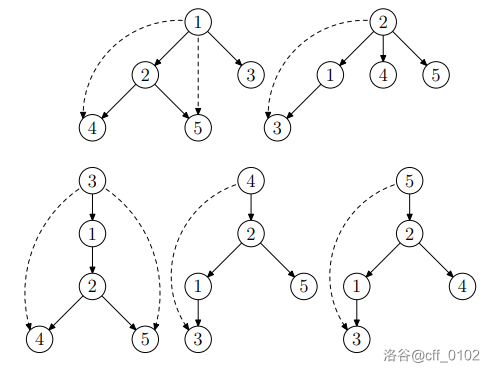
下图给出了第一个样例的图片。虚线表示添加的边。对于顶点 1 和 2,最小可达性为 1;对于顶点 3,4 和 5,最小可达性为 2。
| 子任务 |
分值 |
特殊性质 |
| 1 |
5 |
ui=i,vi=i+1,t=0 |
| 2 |
k=1,n≤2000,t=0 |
| 3 |
10 |
k=1,t=0 |
| 4 |
5 |
ui=i,vi=i+1 |
| 5 |
n≤16 |
| 6 |
10 |
n≤50 |
| 7 |
n≤400 |
| 8 |
n≤2000 |
| 9 |
25 |
n×k≤50000 |
| 10 |
15 |
无 |
对于 100% 的数据,2≤n≤2×105,1≤k≤n−1,n×k≤2×105,0≤t≤1,1≤ui,vi≤n。

