#P11120. [ROIR 2024] 登机 (Day 1)
[ROIR 2024] 登机 (Day 1)
题目背景
翻译自 ROIR 2024 D1T1。
飞机上一共有 排座位,每排有六个位置,其中第三和第四个位置之间有过道。一些乘客在线上已经提前订好位置,其他乘客则在机场的登记台购买机票。在线上购买机票时,乘客可以选择任何座位,且不能更改。例如,当 时,在线上已经订好的座位可能如下(用叉号标记已占用的座位):

有 名乘客在登记台购买机票。根据航空公司的规定,在工作人员帮他们选好位置后,最终的座位安排相对于过道应该是对称的。即,如果某一排的第一个座位有乘客,那么同一排的第六个座位也必须有乘客。同样,第二和第五、第三和第四个座位也必须相应对称。同时,在线上购买的乘客的座位不能改变。在上图的初始座位中,可以添加七名乘客以满足对称性,如下图:
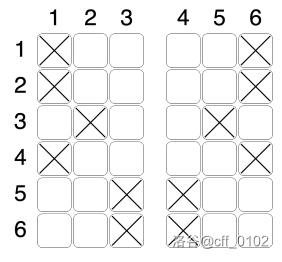
题目描述
给定在线购买的乘客选定的座位,你需要安排 名乘客,使得最终的座位安排相对于过道是对称的。如果不可能做到,输出 Impossible。
输入格式
第一行包含两个整数 和 ,分别表示飞机座位的排数和在机场登记台购买机票的乘客数量(,)。
接下来的 行描述了在线购买的乘客选定好的座位。每行包含六个字符,其中第 行的第 个字符表示第 排的第 个座位的状态,如果第 个座位被占用,则为 X,否则为 .。
输出格式
如果无法找到满足要求的座位安排,输出 Impossible。
否则,输出 行,每行六个字符,即飞机的最终座位安排,其中第 行的第 个字符表示第 排的第 个座位的状态。如果座位被占用则为 X,否则为 .。如果存在多个方案,可以输出其中任意一个。
1 0
X.XX.X
X.XX.X
2 1
X.XX.X
..X...
X.XX.X
..XX..
3 2
X.XX.X
......
X..X.X
Impossible
1 103
.X.XXX
Impossible
6 7
X.....
......
....X.
X.....
......
..XX..
X....X
X....X
.X..X.
X....X
..XX..
..XX..
提示
| 子任务 | 分值 | 特殊性质 |
|---|---|---|
| 同样例 | ||
| 刚开始飞机上所有座位都是空的 | ||
| 刚开始飞机上只有一个座位 | ||
| 无 | ||
对于 的数据,,。
Subtask 5 的最后两个测试点是原数据中没有的 hack。
