#P11107. [ROI 2023] Ultra mex (Day 1)
[ROI 2023] Ultra mex (Day 1)
题目背景
翻译自 ROI 2023 D1T4。
假设 是一个非负整数的集合。将 中不存在的最小非负整数记为 。例如,。
我们还定义了一种在含有 的集合 上的操作,称为 。假设 ,因为 ,显然 。按照以下方法构建新的集合 :对 中的每个元素异或 。例如,$\operatorname{Ultra}(\{0, 1, 2, 4, 5, 9\}) = \{0\oplus2, 1\oplus2, 2\oplus2, 4\oplus2, 5\oplus2, 9\oplus2\} = \{2, 3, 0, 6, 7, 11\} = \{0, 2, 3, 6, 7, 11\}$。
不难发现,如果集合 包含 ,则集合 也包含 。
我们选择由 到 之间的整数组成的集合 ,且 在 中。考虑以下序列:
- $m_0 = \operatorname{mex}(A_0),A_1 = \operatorname{Ultra}(A_0)$。
- $m_1 = \operatorname{mex}(A_1),A_2 = \operatorname{Ultra}(A_1)$。
- $m_i = \operatorname{mex}(A_i),A_{i+1} = \operatorname{Ultra}(A_i)$。
如果从某个数 开始,数字 不再变化,也就是说,对于所有 ,,则称集合 是 mex-stable 的,将 称为集合 的 mex-limit。
题目描述
给定整数 ,计算满足以下条件的集合 的数量:
- 它包含从 到 的 个不同整数(其中 必须包含在 中);
- 它是 mex-stable 的;
- 它的 mex-limit 等于 。
由于答案可能很大,输出答案对 取模后的结果。保证 能被 ()整除。
输入格式
第一行包含一个整数 ,表示要对其取模的模数( 且 可被 整除)(所以 实际上不可能小于 )。保证 是一个质数。
第二行包含一个整数 ,表示输入数据的组数()。
对于每组输入数据,包含三个整数 (,)。
输出格式
对于每组输入数据,输出一行,包含一个整数,表示满足条件的集合 的数量对 取模后的结果。
998244353
6
3 2 1
3 2 2
3 2 3
3 2 4
3 5 1
4 6 1
6
1
0
0
29
2461
提示
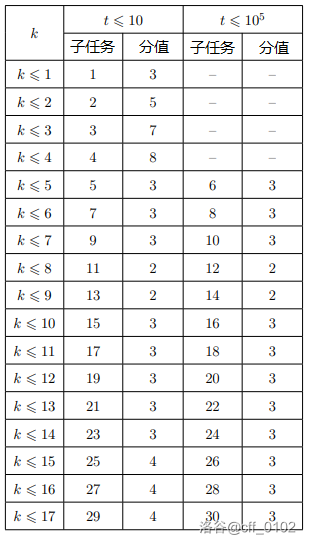
除样例外,本题有三十个子任务,如下图所示。