#P11098. [ROI 2022] 滑梯 (Day 1)
[ROI 2022] 滑梯 (Day 1)
题目描述
翻译自 ROI 2022 D1T3。
佩奇和她的弟弟乔治来到水上公园。乔治喜欢从滑梯上滑行,这个滑梯可以用三角网格的一部分来描述,其中的顶点是滑梯的节点。在每个节点上,可以选择继续沿着哪个管道前进——向左下或向右下。滑梯从上到下编号,从 层开始。在第 层,滑梯只有一个节点,在第 层有两个节点,在第 层有 个节点。总共有 层。每次从上到下滑都要经过恰好 个管道。每个节点都有坐标,用两个数字 表示在第 层中从左边开始数的第 个节点 ()。请注意,每层和每层上的节点都是从 开始编号的。如果乔治位于节点 并向左下滑,他将进入节点 ,如果他向右下滑,他将进入节点 。
这是一个有 层()的滑梯:
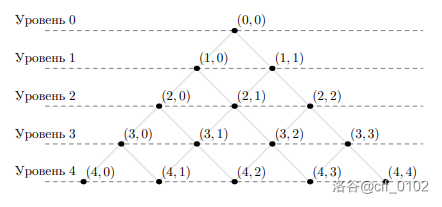
乔治想要从滑坡上滑下 次。在每次下滑之前,佩奇会给他一个指令,告诉他如何沿着滑坡滑行。每个指令由恰好 个命令组成,要么是“向左下”,要么是“向右下”。乔治根据佩奇的命令从当前节点去往下一个节点。第一条指令只有“向右下”的命令。佩奇懒得想出新的指令,因此相邻两次下滑的指令只有一条命令不同:为了从第 条指令得到第 条指令,需要将第 个(不是第 个)命令从“向右下”更改为“向左下”。每个命令只会被更改一次。到最后,第 条指令将只包含“向左下”命令。可以证明,在这 次下滑中,乔治会经过滑梯的每个节点(但不是每个管道)。
在从水上乐园返回的途中,乔治遇到了以下问题。首先,考虑所有他滑过的管道的集合。给出两个节点的坐标: 和 。你需要确定一个节点的坐标 ,使得从这个节点开始,通过这些他滑过的管道可以访问到节点 和节点 ,并且在所有这样的节点中,它是最低的,即 的值最大。可以证明,这样的节点总是存在且唯一。
乔治有很多个问题,但是因为他已经离开了水上乐园,所以他不能碰这个滑梯。他需要你帮忙回答他的所有问题!
输入格式
第一行给出一个整数 ()。
在第二行中,给出 个整数 (),其中 是第 次下滑后将要更改的命令的编号。保证所有的 都是不同的。
在第三行中给出一个整数 (),表示乔治的问题数量。
在接下来的 行中,每行给出四个整数 (,,),表示第 个问题的两个节点的坐标。
输出格式
输出 行,每行输出两个整数 和 ,作为第 个问题的答案的节点坐标。
3
2 3 1
5
3 3 3 0
2 2 2 1
1 0 3 1
3 1 3 2
2 2 2 2
0 0
1 1
0 0
2 1
2 2
提示
样例解释:
乔治四次滑滑梯的路线是这样的:
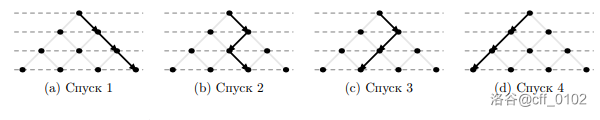
所以所有他经过的管道的集合是这样的:
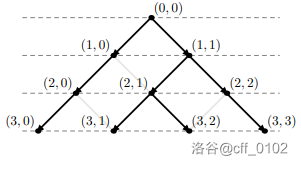
五个问题的答案看图易得。
数据范围:
| Subtask | 分值 | 特殊性质 | ||
|---|---|---|---|---|
| 对于所有 , | ||||
| 数组 有特殊形式 | ||||
Subtask 4 中,数组 形如 ,其中 。
