#P11093. [ROI 2021] 树制游戏 (Day 2)
[ROI 2021] 树制游戏 (Day 2)
题目描述
翻译自 ROI 2021 D2T2。
Vasya 最近想到了一种新的娱乐方式。他想让一个有 个顶点和 条边的有向连通图成为他的玩具。这个图满足以下条件:对于图中的每条边 ,都存在一条反向的边 。换句话说,这个图是由一棵树转化而来的,其中每条无向边都被分成两个方向相反的边。
Vasya 将这样一对边 称为“gadget”,其中 的终点与 的起点相同,或者 的终点与 的起点相同(特别地,两条方向相反的边也是一种“gadget”)。简单来说,“gadget”就是一条长度为 的路径。Vasya 的娱乐方式是将图中的边划分为互不相交的“gadget”。当然,对于原始图来说,这很容易做到。
但是,Vasya 的好朋友 Petya 从树中删除了 条有向边,使得图中剩下 条有向边。
现在 Vasya 想知道是否可以将剩下的边划分为互不相交的“gadget”,如果可能的话,还要找出这种划分的方法。
输入格式
第一行包含两个整数 和 ,分别表示顶点数和剩余边数。保证 是偶数。
接下来的 行,每行包含两个整数 和 ,表示剩余边的起点和终点。
输出格式
如果无法将边分成“gadget”,则输出 No。
否则,输出 Yes,然后输出 行,每行包含 个数字,表示每个“gadget”中的两对边。每条边由起点和终点两个数字表示。
5 6
1 2
2 1
1 5
2 3
2 4
4 2
Yes
1 2 2 3
2 1 1 5
2 4 4 2
4 4
2 1
2 3
2 4
4 2
No
4 4
1 2
2 1
3 4
4 3
Yes
1 2 2 1
3 4 4 3
提示
第一个示例中的“gadget”划分如下图所示,同一个类型的两条线组成了一个“gadget”。
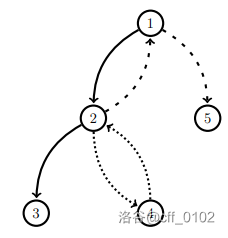
对于 的数据,$2 \le n \le 150000,2 \le m \le 2\times n - 2,1 \le u_i, v_i \le n$。
| 子任务 | 分值 | 的特殊性质 | |
|---|---|---|---|
| 无 | |||
| 无 | |||
| 无 |
