#P11054. [IOI 2024] 斯芬克斯的谜题
[IOI 2024] 斯芬克斯的谜题
题目背景
请在提交时不要引用 sphinx.h,并在代码开头加入如下内容:
#include <vector>
int perform_experiment(std::vector<int> E);
请勿用 C++14 (GCC 9) 提交。
题目描述
斯芬克斯为你准备了一个谜题。给定 个顶点的图,顶点从 到 编号。图中有 条边,从 到 编号。每条边连接两个不同的顶点,且边是双向的。具体来说,对从 到 的每个 ,边 连接顶点 和 。任意两个顶点之间最多有一条边。若两个顶点被一条边连接,则它们是相邻的。
对顶点序列 (对 ),若每两个连续顶点 和 (对所有满足 的 )是相邻的,则称其为一条路径。路径 连接顶点 和 。在给定的图中,每对顶点被某条路径连接。
现在有 种颜色,从 到 编号。其中,颜色 是特殊的,称为斯芬克斯之色。一开始每个顶点都有一种颜色,顶点 ()的颜色是 。多个顶点可以是同一种颜色的,有的颜色可能没有对应的顶点,且不会有顶点的颜色是斯芬克斯之色。也就是说,()。
若一条路径 (对 )上的所有顶点都是相同颜色的,则称其是单色的。也就是说,满足 (对所有满足 的 )。此外,两个顶点 和 (,)在同一个单色分支中,当且仅当它们被某条单色路径连接。
你知道图中顶点和边的关系,但是你不知道每个顶点的颜色。你希望通过重新着色实验来弄清楚顶点的颜色。
在一次重新着色实验中,你可以对任意多的顶点进行重新着色。具体来说,在一次重新着色实验中,你先给出一个长度为 的数组 ,对每个 (), 的值在 和 之间(包括 和 )。重新着色后,每个顶点 的颜色变成了 ,其中 的值:
- 若 ,则是 ,也就是重新着色前顶点 的颜色;
- 否则,是 。
注意:你可以在重新着色的过程中使用斯芬克斯之色。
在将每个顶点 的颜色设为 ()之后,斯芬克斯会宣布图中单色分支的数量。新的着色情况仅在本次重新着色实验中有效,因此当本次实验结束后,所有顶点的颜色会恢复成最初的情况。
你的任务是至多通过 次重新着色实验来确定图中顶点的颜色。如果正确给出了每对相邻顶点是否具有相同颜色,那么也会获得部分分数。
实现细节
你要实现以下函数。
std::vector<int> find_colours(int N,
std::vector<int> X, std::vector<int> Y)
- :图中顶点的数量。
- ,:两个长度为 的数组,描述图中的边。
- 该函数应该返回一个长度为 的数组 ,表示图中顶点的颜色。
- 对每个测试用例,该函数恰好被调用一次。
以上函数可以通过调用下面的函数来进行重新着色实验:
int perform_experiment(std::vector<int> E)
- :长度为 的数组,指定顶点重新着色的方式。
- 该函数返回根据 所给出的方式进行重新着色后单色分支的数量。
- 该函数至多只能调用 次。
评测程序不是自适应的。也就是说,顶点的颜色在调用 find_colours 之前就已经固定下来了。
输入格式
评测程序示例读取如下格式的输入:
N M
C[0] C[1] ... C[N-1]
X[0] Y[0]
X[1] Y[1]
...
X[M-1] Y[M-1]
输出格式
评测程序示例按照如下格式打印你的答案:
L Q
G[0] G[1] ... G[L-1]
这里, 是 find_colours 返回的数组 的长度, 是调用 perform_experiment 的次数。
4 4
2 0 0 0
0 1
1 2
0 2
0 3
4 3
2 0 0 0
提示
考虑以下函数调用。
find_colours(4, [0, 1, 0, 0], [1, 2, 2, 3])
在这个例子中,假设顶点的(隐藏的)颜色是 ,如下图所示。顶点的颜色同时也用数字标注在顶点右上角的标签里。
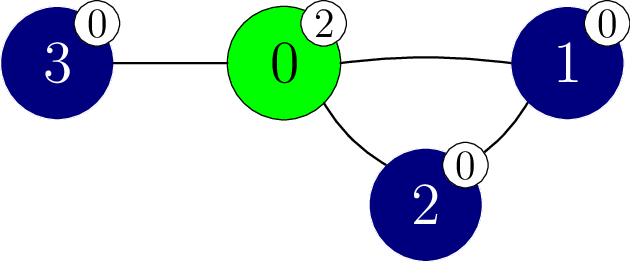
假设该函数以下列方式调用 perform_experiment。
perform_experiment([-1, -1, -1, -1])
这次调用没有重新着色任何顶点,因此所有顶点都保持它们原来的颜色。
顶点 和顶点 都是颜色 的。因此路径 是单色路径,从而顶点 和顶点 在同一个单色分支中。
顶点 和顶点 都是颜色 的。但是由于不存在连接它们的单色路径,因此它们在不同的单色分支中。
总共有 个单色分支,分别是顶点集合 、 和 。因此,本次函数调用返回 。
再假设该函数以下列方式调用 perform_experiment。
perform_experiment([0, -1, -1, -1])
这次调用只把顶点 重新着色成颜色 ,结果如下图所示。
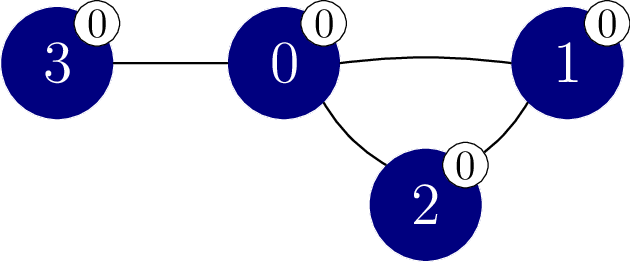
此时所有顶点都属于同一个单色分支,因此本次函数调用返回 。由此可以推断顶点 、 和 都是颜色 的。
假设该函数还以下列方式调用 perform_experiment。
perform_experiment([-1, -1, -1, 2])
这次调用把顶点 重新着色成颜色 ,结果如下图所示。
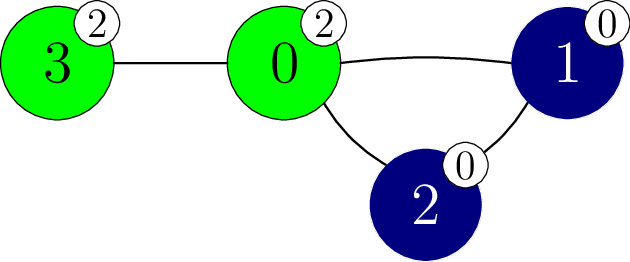
这时有 个单色分支,分别是顶点集合 和 ,因此本次函数调用返回 。由此可以推断顶点 是颜色 的。
然后函数 find_colours 返回数组 。由于 ,因此可以获得满分。
此外,也还有多种返回值,例如 或 ,可以获得 的分数。
约束条件
- 对所有满足 的 ,都有 。
- 对所有满足 的 和 ,都有 或 。
- 每对顶点被某条路径连接。
- 对所有满足 的 ,都有 。
| 子任务 | 分数 | 额外的约束条件 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | 给定的图是一条路径:,且顶点 和 是相邻的()。 | |
| 4 | 给定的图是完全图:,且任意两个顶点是相邻的。 | |
| 5 | 没有额外的约束条件。 |
在每个子任务中,如果你的程序正确给出了每对相邻顶点是否具有相同颜色,那么也会获得部分分数。
更准确地说,如果在所有测试用例中 find_colours 返回的数组 与数组 完全一样(也就是对所有满足 的 ,都有 ),你会获得该子任务的全部分数。否则,如果在某个子任务的所有测试样例中满足下列条件,你会获得该子任务 的分数:
- 对所有满足 的 ,都有 ;
- 对所有满足 的 ,都有:
- 当且仅当 。
