题目描述

Happybob 想做一块煎饼，他决定在一个 $n$ 行 $n$ 列的斜正方形的锅里做一个煎饼，所以煎饼的大小不能超过斜正方形的大小。

由于原料有限，因此 Happybob 的煎饼必须是 $m$ 个长方形覆盖而成的。

Happybob 想知道，他能制作出的最大的煎饼的面积是多少。

---

形式化题意：

用 $m$ 个长方形覆盖大小为 $n$ 的斜正方形，最多覆盖多少个格子？

斜正方形和覆盖的定义见说明/提示。

输入格式

第一行，一个整数 $T$，表示询问数。

接下来 $T$ 行，每行两个整数 $n,m$，表示一次询问。

输出格式

$T$ 行，每一行表示一个询问的答案。

3
5 1
6 2
8 2

9
20
32

提示

样例说明

三次询问的方案是：

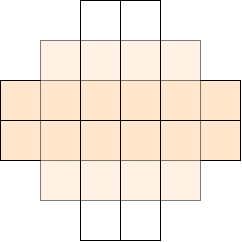
（方案不唯一）

数据范围

$1\le T\le 50$，$1\le n\le 2\times 10^9$，$1\le m\le\lceil\dfrac{n}{2}\rceil$。

---

形式化定义

斜正方形的定义：

更形式化地，建立直角坐标系，定义一个大小为 $n$ 的斜正方形的中心为原点。

若 $n$ 为奇数，则该斜正方形可以描述为所有以 $\big\{(x, y) \big | |x| + |y| \le \lfloor \frac{n}{2} \rfloor \text{ and } x, y \in \Z\big\}$ 中的点为正方形中心的边长为 $1$ 的正方形格子组成的组合图形。

若 $n$ 为偶数，则该斜正方形可以描述为所有以 $\big\{(x, y) \big | |x| + |y| \le \frac{n}{2} \text{ and } (x + \frac{1}{2}), (y + \frac{1}{2}) \in \Z\big\}$ 中的点为正方形中心的边长为 $1$ 的正方形格子组成的组合图形。

一个 $n=5$ 的斜正方形（淡蓝色为格子中心）：

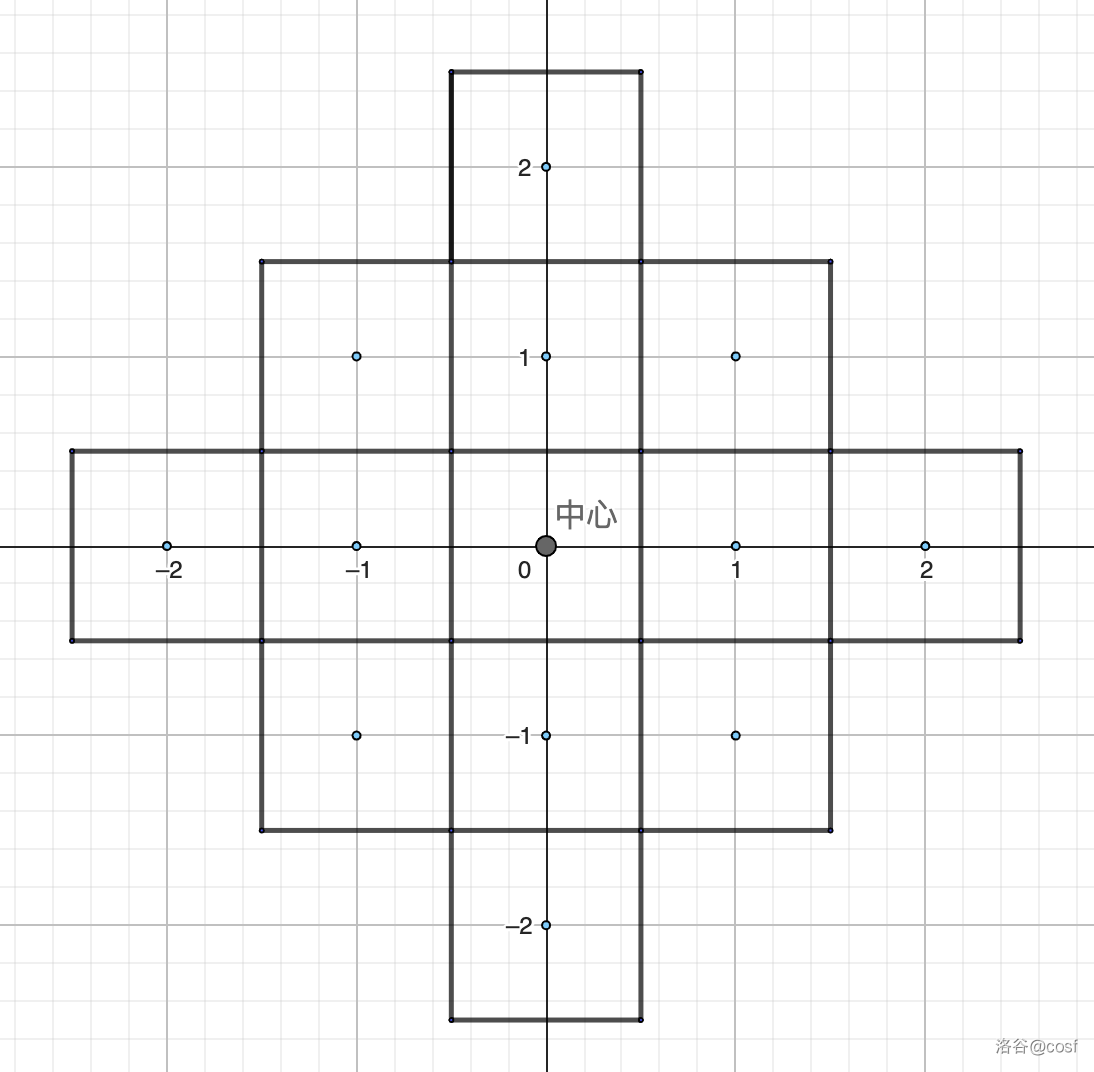
一个 $n=6$ 的斜正方形（淡蓝色为格子中心）：

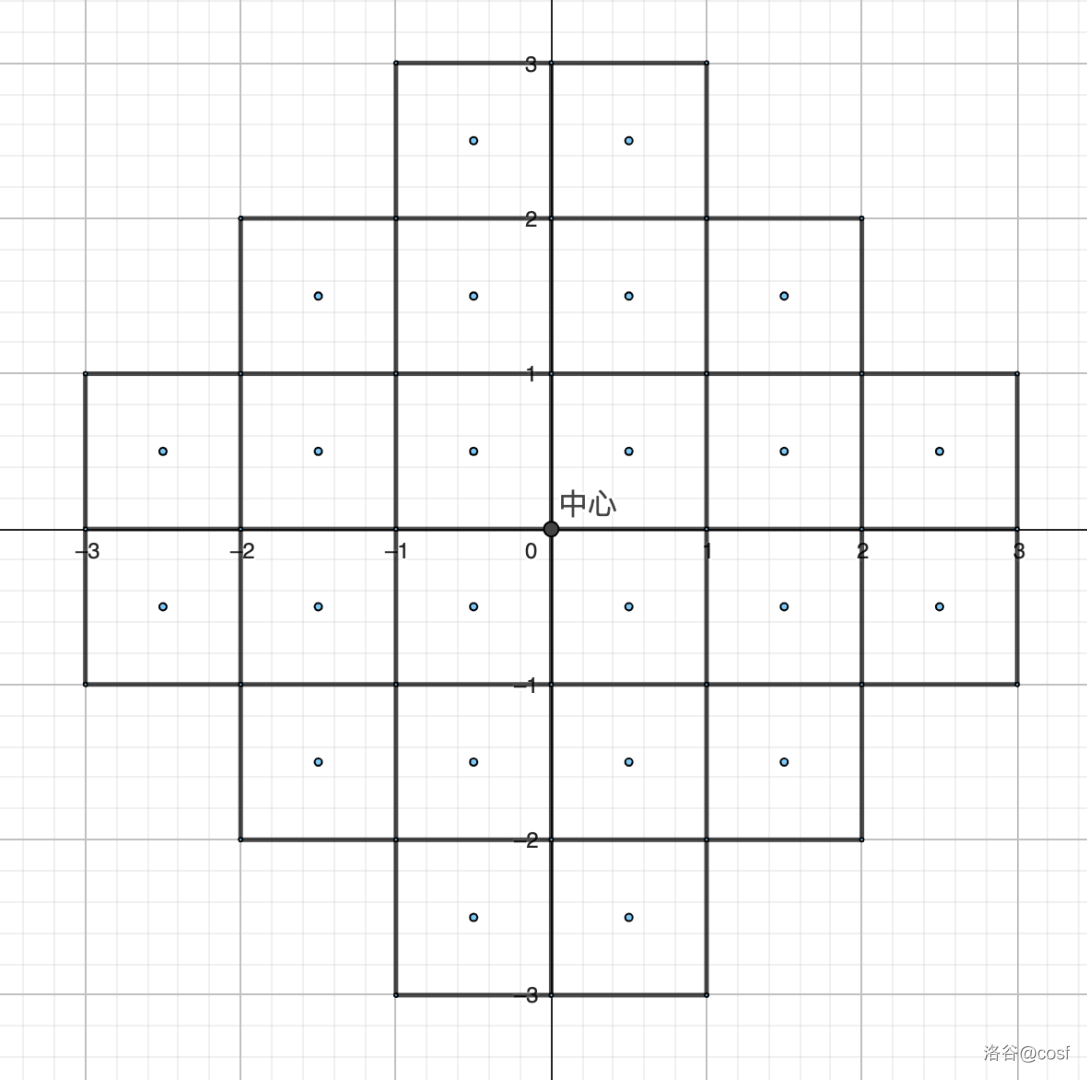
覆盖方法的定义：

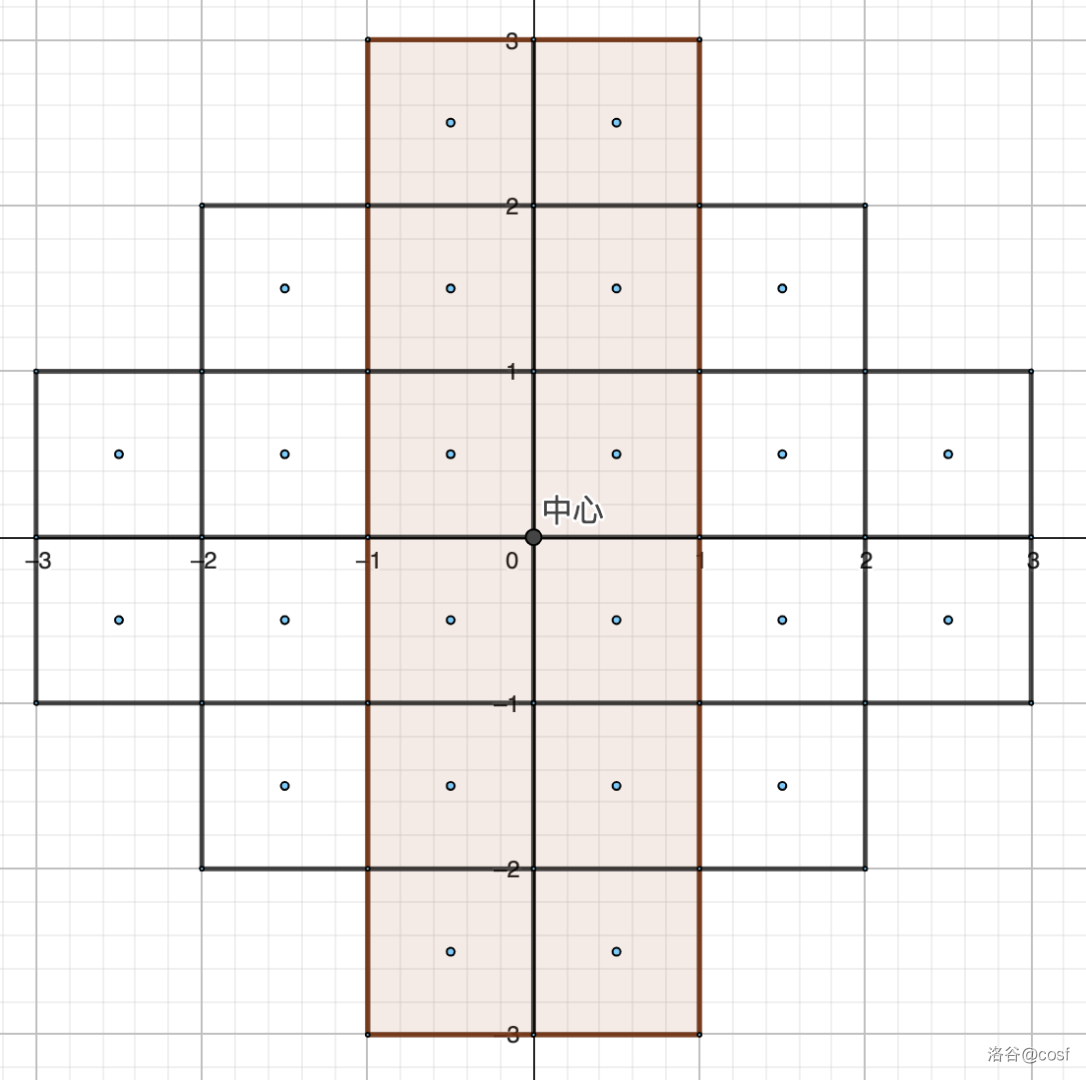
定义一个长方形 $R$ 覆盖该斜正方形，当且仅当 $R$ 为由若干格子组成的长方形。

下面是一个覆盖斜正方形的长方形：

下面则不是覆盖斜正方形的长方形：

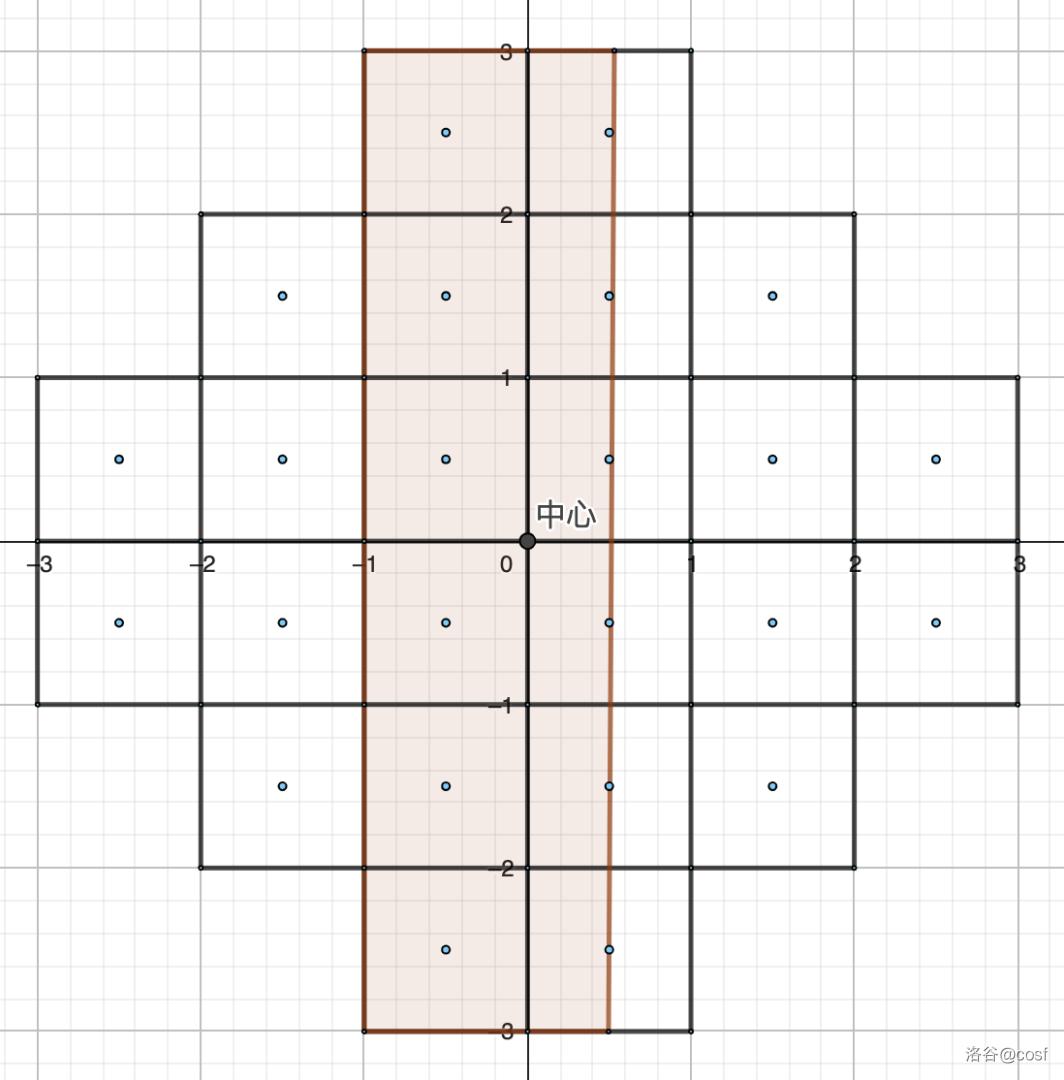
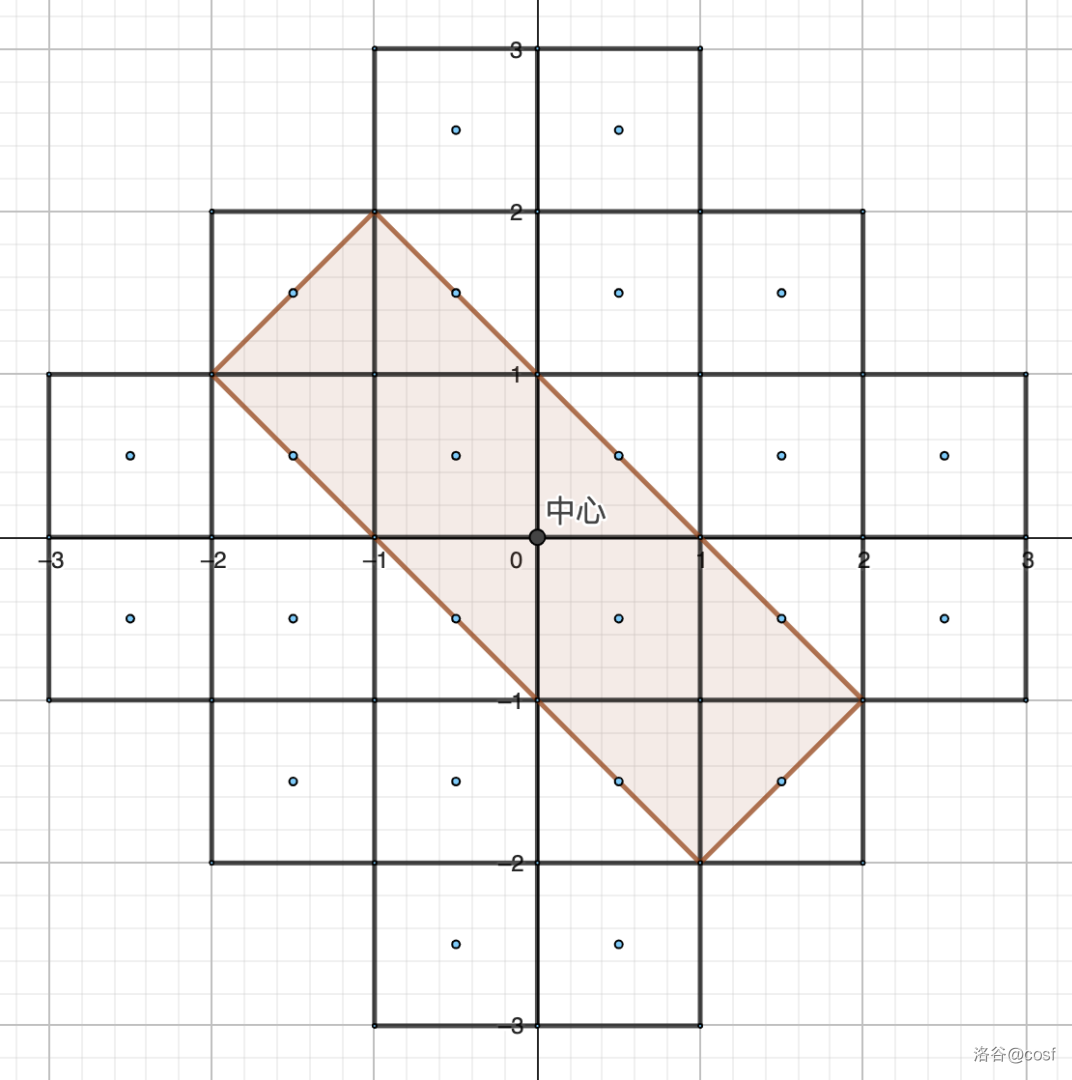
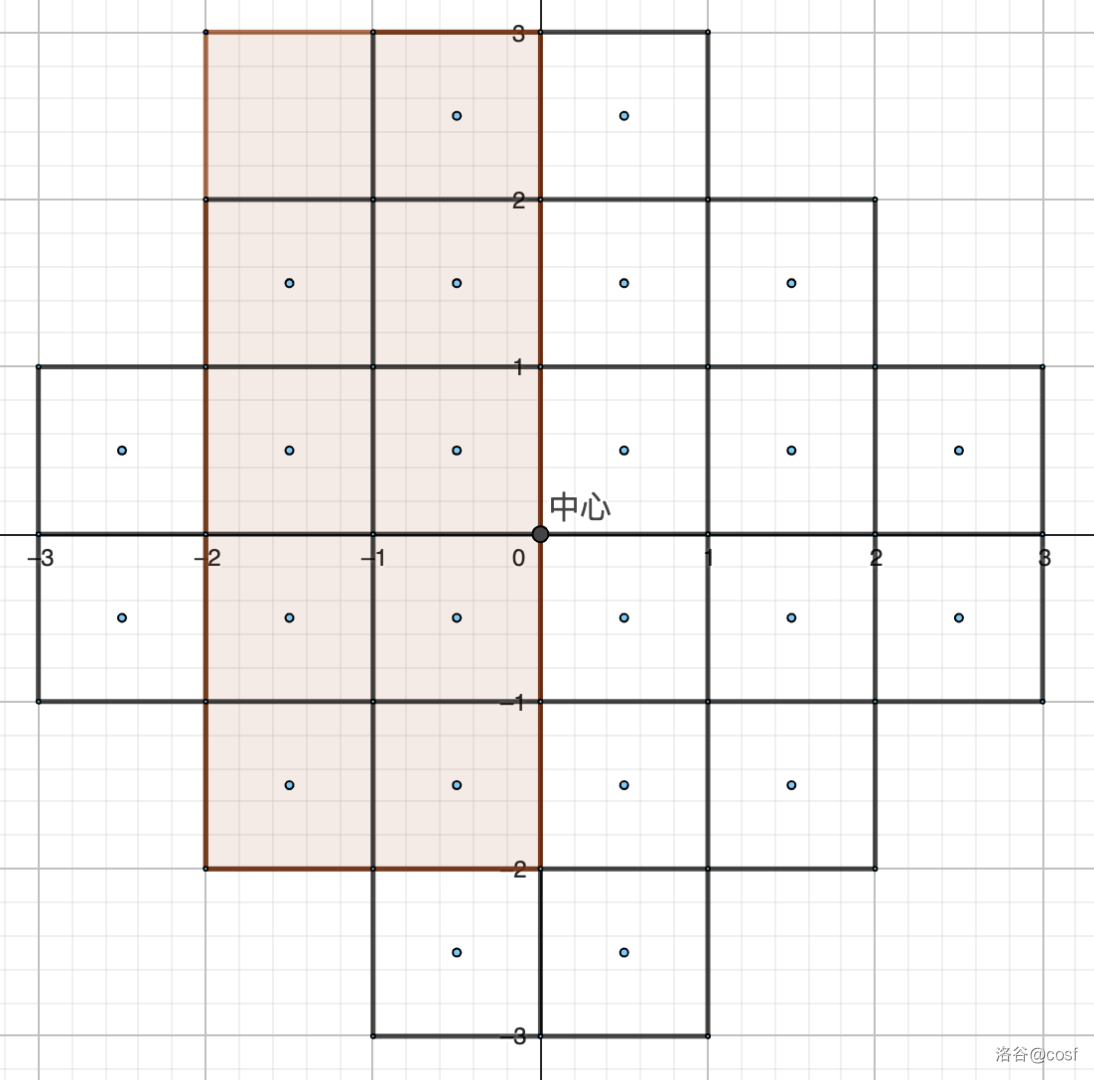
定义一个格子被覆盖，当且仅当选择的 $m$ 个覆盖斜正方形的长方形中有至少一个完全包含该格子。