#P10850. [EGOI 2024] Light Bulbs / 灯泡安装
[EGOI 2024] Light Bulbs / 灯泡安装
题目背景
Day 2 Problem C.
题面译自 EGOI2024 lightbulbs。翻译来自于 ChatGPT 并进行人工校对,若有误请联系 rui_er。
本题是一道交互题。
题目描述
在 1891 年在埃因霍温创立他的灯泡公司后不久,Frederik Philips 取得了一个伟大的发现:可以在水平方向或垂直方向上点亮无限射线的灯泡。凭借这一新发现,他希望革新现代家庭的室内设计。
他和他的儿子 Gerard 计划进行一个复杂的安装。他们在一个房间内的 网格中安装了 个灯泡。他们希望尽可能少地打开灯泡来点亮整个房间,以节省电力。每个灯泡要么是垂直的,意味着它点亮其列中的所有格子,要么是水平的,意味着它点亮其行中的所有格子。
下图显示了一个垂直灯(左)和一个水平灯(右)的示例。
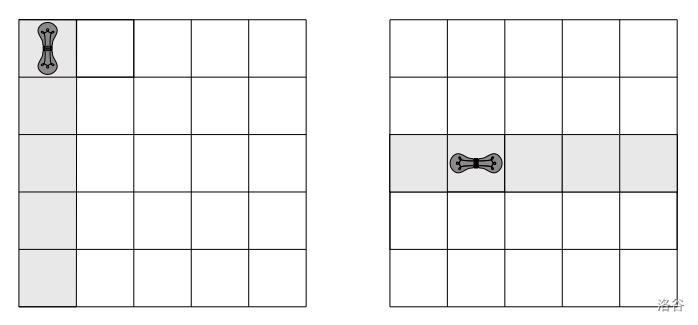
不幸的是,他们在安装灯泡时没有注意,不记得哪些灯泡是水平点亮的,哪些是垂直点亮的。相反,他们进行了些实验来弄清楚使用哪些灯泡可以点亮整个房间。Gerard 留在有灯泡的房间里,而 Frederik 在另一个房间操作开关。
在每次实验中,Frederik 会打开或关闭每个灯泡,而 Gerard 会报告点亮了多少个格子;由两个或更多独立灯泡点亮的格子只算作一次。实验期间打开多少灯泡并不重要,但他们时间紧迫,理想情况下希望尽可能少地进行实验。
帮助他们找到一种使用最少灯泡点亮整个房间的安排。他们最多可以进行 次实验。然而,如果他们使用更少的实验次数,你将获得更高的分数。
交互方式
本题是一道交互题。
- 你的程序应首先读取一个整数 ,即网格的高度和宽度。
- 然后,程序应与评测系统进行交互。进行实验时,你应首先打印一行问号
?。在接下来的 行中,输出一个 的网格,指定哪些灯泡被点亮。具体来说,在每行中,输出一个长度为 的字符串,由 (关闭)和 (打开)组成。然后,程序应读取一个整数 (),表示通过指定的灯泡点亮的格子数量。 - 当你想要回答时,打印一行感叹号
!,后跟 行,格式与上面相同。在你的回答被接受前,灯泡必须点亮整个网格,且打开的灯泡数量必须最少。
之后,你的程序应退出。
评测系统是非自适应的,这意味着灯泡网格在交互开始前已经确定。
每次进行实验后,请确保刷新标准输出;否则,程序可能会被判定为 TLE。在 Python 中,只要使用 input() 读取行,就会自动刷新。在 C++ 中,cout << endl; 除了打印换行符外还会刷新;如果使用 printf,请使用 fflush(stdout)。
输入格式
见【交互方式】部分。
输出格式
见【交互方式】部分。
5
10
13
?
11000
00000
00000
00000
00000
?
01000
01000
01000
00100
00000
!
00100
00010
01000
00001
01000
提示
样例解释
在样例交互中,程序首先读取网格大小 。下图展示了隐藏的网格(程序不知道)和众多可能答案之一,使用五盏灯点亮整个网格。标记的灯是打开的,较暗的方块是被照亮的。
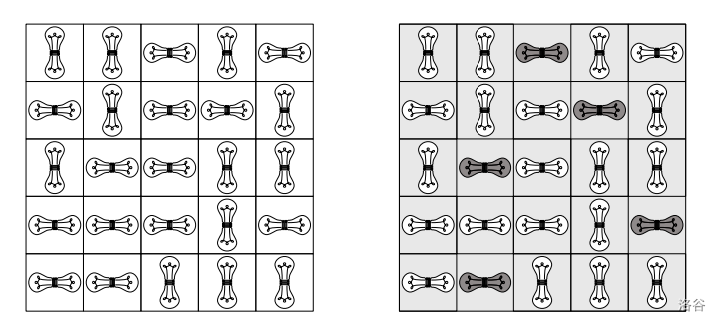
程序进行了如下所示的两个实验。在第一个实验中,使用左上角的两个垂直灯照亮了总共 10 个方块。第二个实验照亮了总共 13 个方块。最后,程序写出了它的答案(如上图所示)并退出。

数据范围
对于全部数据,。你最多可以进行 次实验(输出最终答案不计入实验次数)。如果你超过了限制,程序会被判定为 WA。
- 子任务一( 分):。
- 子任务二( 分):。
- 子任务三(至多 分):无特殊限制。
注:部分测试点在 EGOI 中被放在多个子任务中。为节省评测资源及整理数据的工作量,这些测试点被放在包含它的所有子任务中编号最小的一个。这可能导致一份代码得到比预期更高的分数,但是无法过题。
评分方式
在子任务三中,你按照下面的公式根据进行实验的次数得分:
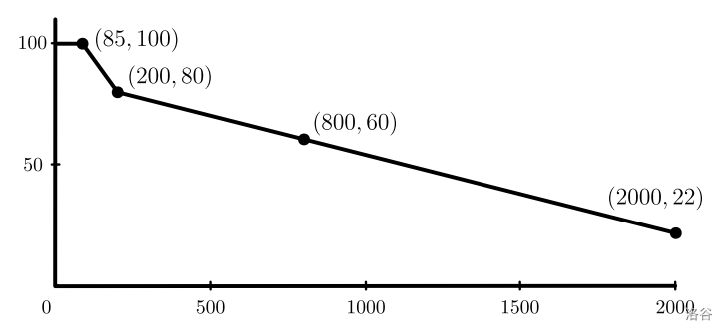
$$\textrm{score}= \begin{cases} (2000-Q)\cdot 29/900&\text{if }200\le Q\le 2000\\ 58+(200-Q)\cdot 4/23&\text{if }85\le Q\le 200\\ 78&\text{if }Q\le 85\\ \end{cases} $$其中 是这个子任务的所有测试点中最多的实验次数。你的得分将被取整到最接近的整数。
下面是总分关于子任务三中 的函数图象。要想得到满分,你需要进行不超过 次实验解决子任务三中的每个测试点。