[POI 2020/2021 R3] Droga do domu
You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.
题目背景
译自 XXVIII Olimpiada Informatyczna - III etap Droga do domu。
d1t1。
题目描述
个点, 条边,无重边自环,边有长度。
号点是学校, 号点是家。
条公交线路。公交逢点必停,且一个点不会停两次。在一条边上行驶的时间就是它的长度。给定了第一班公交发车时间和发车间隔。
在时刻 从学校出发,至多换乘 次,求最早什么时候到家。
只计算路上时间和等车时间。换乘时间不计。
输入格式
第一行:五个整数 。
接下来 行:每行三个整数 ,表示有一条边连接 ,长度为 。
接下来 行:每两行描述一条公交线路:
- 第一行三个整数 ,表示它共停靠 个点,第一班在时刻 发车,每两班之间时间间隔为 。
- 第二行 个整数 ,依次为它停靠的 个点。
输出格式
一行一个整数,答案。
如果不能到家,那么输出一行一个字符串 NIE。
4 4 2 1 1
1 2 2
2 3 4
1 3 3
4 3 2
4 0 10
1 2 3 4
3 2 7
1 3 2
8
10 45 17 10 123
1 2 1
1 3 100
1 4 100
1 5 100
1 6 100
1 7 100
1 8 100
1 9 100
1 10 100
2 3 1
2 4 100
2 5 100
2 6 100
2 7 100
2 8 100
2 9 100
2 10 100
3 4 1
3 5 100
3 6 100
3 7 100
3 8 100
3 9 100
3 10 100
4 5 1
4 6 100
4 7 100
4 8 100
4 9 100
4 10 100
5 6 1
5 7 100
5 8 100
5 9 100
5 10 100
6 7 1
6 8 100
6 9 100
6 10 100
7 8 1
7 9 100
7 10 100
8 9 1
8 10 100
9 10 1
2 0 1
1 2
2 0 1
1 3
2 0 1
2 3
2 0 1
2 4
2 0 1
3 4
2 0 1
3 5
2 0 1
4 5
2 0 1
4 6
2 0 1
5 6
2 0 1
5 7
2 0 1
6 7
2 0 1
6 8
2 0 1
7 8
2 0 1
7 9
2 0 1
8 9
2 0 1
8 10
2 0 1
9 10
132
见附件
1000000102
见附件
11100000071
提示
样例解释: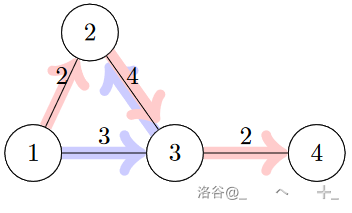
对于全部数据,,,,,,,,,,,。
| 子任务编号 | 限制 | 分数 |
|---|---|---|
| 1 | 20 | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
