分类

$\color{Green}{Easy}$：一眼题。

$\color{Blue}{Median}$：经过思考可以做出来。

$\color{Yellow}{Hard}$：看完题解立马理解。

$\color{Orange}{Insane}$：看完题解经过一段时间的思考能够理解。

$\color{Red}{Supreme}$：看完题解经过长久思考才理解。

CF10D LCIS $\color{Green}{Easy}$

还是最水 *2800。

CF11E Forward, march! $\color{Green}{Easy}$

卡常滚出 OI。

CF19D Points $\color{Blue}{Median}$

原本想到树套树，但是 $n \leq 2 \times 10^5$ 肯定过不去。

仔细想想其实可以线段树二分 + STL set。

CF30E Tricky and Clever Password $\color{Yellow}{Hard}$

我还是太菜了...

首先容易想到枚举 $b$，因为 $n$ 要满足最大。

然后就是枚举 $a'$，这里要观察到 $a$ 的位置随着 $|a'|$ 的增大单调不降，然后就可以哈希乱搞了。

CF48F Snow sellers $\color{Blue}{Median}$（思考） / $\color{Yellow}{Hard}$（写代码）

傻逼 Luogu 翻译又不放数据范围。

首先 $O(n m \log m)$ 的贪心过于显然，然后考虑使用类似线段树二分的策略，可以做到 $ O(n (m + \frac{m}{2} + \frac{m}{4} + \cdots)) = O(n m) $。

需要卡常，卡精度和使用 STL nth_element，所以我 copy 题解不过分吧。

CF74E Shift It! $\color{Blue}{Median}$

？？？为什么都喜欢考魔方题。

使用上下右左上交换相邻数字即可，随便过。

CF77E Martian Food $\color{Yellow}{Hard}$

考虑笛卡尔定理，可以得出：

$$(\sum_{i = 1}^4 \frac{1}{r_i})^2 = 2 \sum_{i = 1}^4 \frac{1}{r_i^2} $$

其中若外切半径取正，否则取负。

可以得出：

$$r_k = 2(r_1 + r_2 + r_{k - 2}) - r_{k - 2}$$

递推即可。

CF79D Password & P3943 星空 $\color{Blue}{Median}$

好题。

考虑差分，然后就可以状压 dp 了。

使用 bfs 预处理代价即可。

CF83E Two Subsequences $\color{Yellow}{Hard}$

建议改名：CSP2024 T3 加强版（但是我没做出来 T3 QAQ）。

考虑 01-Trie + dp，用 01-Trie 维护 dp 结构，每次转移的时候打标记即可。

AT_agc027_d [AGC027D] Modulo Matrix $\color{Yellow}{Hard}$

考虑黑白染色，注意到以下填法：

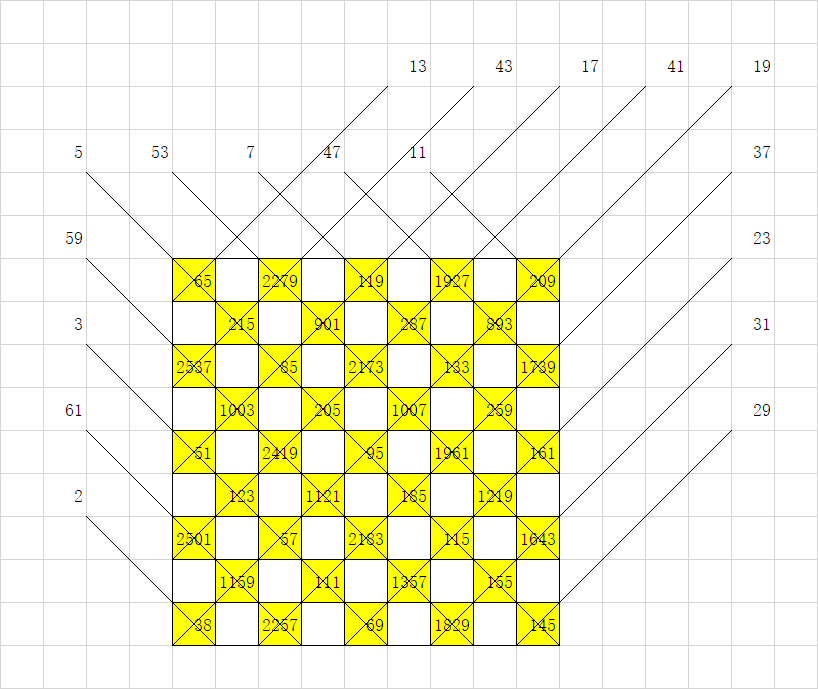
白色填 4 个格子的 lcm + m 即可。

P3045 [USACO12FEB] Cow Coupons G $\color{Green}{Easy}$

还是反悔贪心模版。

给 $i$ 用优惠券比 $j$ 优当且仅当 $p_i - c_i > p_j - c_j$。

然后就是简单的 3 heap 了。

A - What month is it? $\color{Green}{Easy}$

模拟即可。

B - Most Minority $\color{Green}{Easy}$

模拟即可。

C - Sum of Min Query $\color{Green}{Easy}$

模拟即可。

D - Toggle Maze $\color{Green}{Easy}$

bfs 即可。

E - Reachability Query $\color{Green}{Easy}$

并查集即可。

G - sqrt(n²+n+X) $\color{Green}{Easy}$

$n^2 + n + x = k^2$ 转换成 $(2k + 2n + 1)(2k - 2n - 1) = 4 x - 1$ 即可。