1 原版题面
高联班测试
2024年2月22日
-
(40分)设四边形ABCD是圆内接四边形. 设IA,IB,IC,ID是$\triangle ABD,\triangle ABC,\triangle BCD,\triangle ACD$的内心. 设⊙IA,⊙IB,⊙IC,⊙ID分别是$\triangle ABD,\triangle ABC,\triangle BCD,\triangle ACD$的内接圆. 设lAB为圆IA与圆IB不同于AB的外公切线. 设lBC为圆IB与圆IC不同于BC的外公切线. 设lCD为圆IC与圆ID不同于CD的外公切线. 设lDA为圆IA与圆ID不同于AD的外公切线. 设lAB交lAD于点A′, 设lBC交lCD于点C′. 证明:AA′//CC′.
-
(40分)
(a) 是否存在有界无穷实数列{an}(n∈N∗), 满足1=a1≤a2≤…≤an≤an+1≤…, 且对于任意奇数j, 存在k>j, 使得jaj≤kak?
(b) 是否存在有界无穷实数列{an}(n∈N∗), 满足1=a1≤a2≤…≤an≤an+1≤…, 且对于任意完全平方数j, 存在k>j, 使得jaj≤kak?
-
(50分) 求所有正整数n≥2, 使得存在n个正整数ai(1≤i≤n)满足如下条件:i=1∑nai不是n的倍数, 对任意1≤j≤n, 以下n−1个数中至少有一个是n的倍数:
$$a_j,a_j+a_{j+1},\ldots,a_j+a_{j+1}+\ldots+a_{j+n-2}.
$$其中ai+n=ai,∀i∈Z.
-
(50分) 设f是从正整数到正整数到映射, 满足对任意的正整数m,n, 以下f(n)个数中有且仅有一个n的倍数:
f(m+1),f(m+2),…,f(m+f(n)).
证明: f(f(n))=n,∀n∈N∗.
2 优化版题面
高联班测试
2024 年 2 月 22 日
-
(40 分)设四边形 ABCD 是圆内接四边形. 设 IA,IB,IC,ID 是 $\triangle ABD,\triangle ABC,\triangle BCD,\triangle ACD$ 的内心. 设 ⊙IA,⊙IB,⊙IC,⊙ID 分别是 $\triangle ABD,\triangle ABC,\triangle BCD,\triangle ACD$ 的内接圆. 设 lAB 为圆 IA 与圆 IB 不同于 AB 的外公切线. 设 lBC 为圆 IB 与圆 IC 不同于 BC 的外公切线. 设 lCD 为圆 IC 与圆 ID 不同于 CD 的外公切线. 设 lDA 为圆 IA 与圆 ID 不同于 AD 的外公切线. 设 lAB 交 lAD 于点 A′,设 lBC 交 lCD 于点 C′. 证明:AA′//CC′.
-
(40 分)
(a) 是否存在有界无穷实数列 {an}(n∈N∗),满足 1=a1≤a2≤…≤an≤an+1≤…,且对于任意奇数 j,存在 k>j,使得 jaj≤kak?
(b) 是否存在有界无穷实数列 {an}(n∈N∗),满足 1=a1≤a2≤…≤an≤an+1≤…,且对于任意完全平方数 j,存在 k>j,使得 jaj≤kak?
-
(50 分)求所有正整数 n≥2,使得存在 n 个正整数 ai(1≤i≤n) 满足如下条件:i=1∑nai 不是 n 的倍数,对任意 1≤j≤n,以下 n−1 个数中至少有一个是 n 的倍数:
$$a_j,a_j+a_{j+1},\ldots,a_j+a_{j+1}+\ldots+a_{j+n-2}.
$$其中 ai+n=ai,∀i∈Z.
-
(50分)设 f 是从正整数到正整数到映射,满足对任意的正整数 m,n,以下 f(n) 个数中有且仅有一个 n 的倍数:
f(m+1),f(m+2),…,f(m+f(n)).
证明:f(f(n))=n,∀n∈N∗.
3 简化题面
-
(40)圆内接四边形 ABCD 中,$I_A=I_{\triangle DAB},I_B=I_{\triangle ABC},I_C=I_{\triangle BCD},I_D=I_{\triangle CDA}$,⊙IA 指其内切圆,其他同理. lAB 为 ⊙IA 和 ⊙IB 异于 AB 的外公切线,其他同理. lAB∩lDA=A′,lBC∩lCD=C′. 证明:AA′//CC′.
-
(40)
(a) 是否存在有界的实数序列 {an}(n∈N∗),满足 1=a1≤a2≤…≤an≤an+1≤…,且 $\forall j\in\mathbb{N}^*,2\nmid j:\exists k\in\mathbb{N}^*_{>j}:\dfrac{a_j}{j}\le \dfrac{a_k}{k}$?
(b) 将 2∤j 改为 j∈Z,还是否存在?
-
(50) 求 $\forall n\in\mathbb{N}^*_{\ge2}:\exists a_i\in\mathbb{N}^*(1\le i\le n):(n\nmid\sum\limits_{i=1}^na_i$ 且 $\forall j\in\{1,2,\cdots,n\}:\exists k\in\{1,2,\cdots,n-1\}:n\mid\sum\limits_{i=0}^{k-1}a_{j+i})$. 下标循环.
-
(50) 若 f:N∗→N∗ 满足:$\forall m,n\in\mathbb{N}^*:\exists!k\in\{1,2,...,f(n)\}:n\mid f(m+k)$,则 f(f(n))=n,∀n∈N∗.
4 民间解答
Problem 1
a3
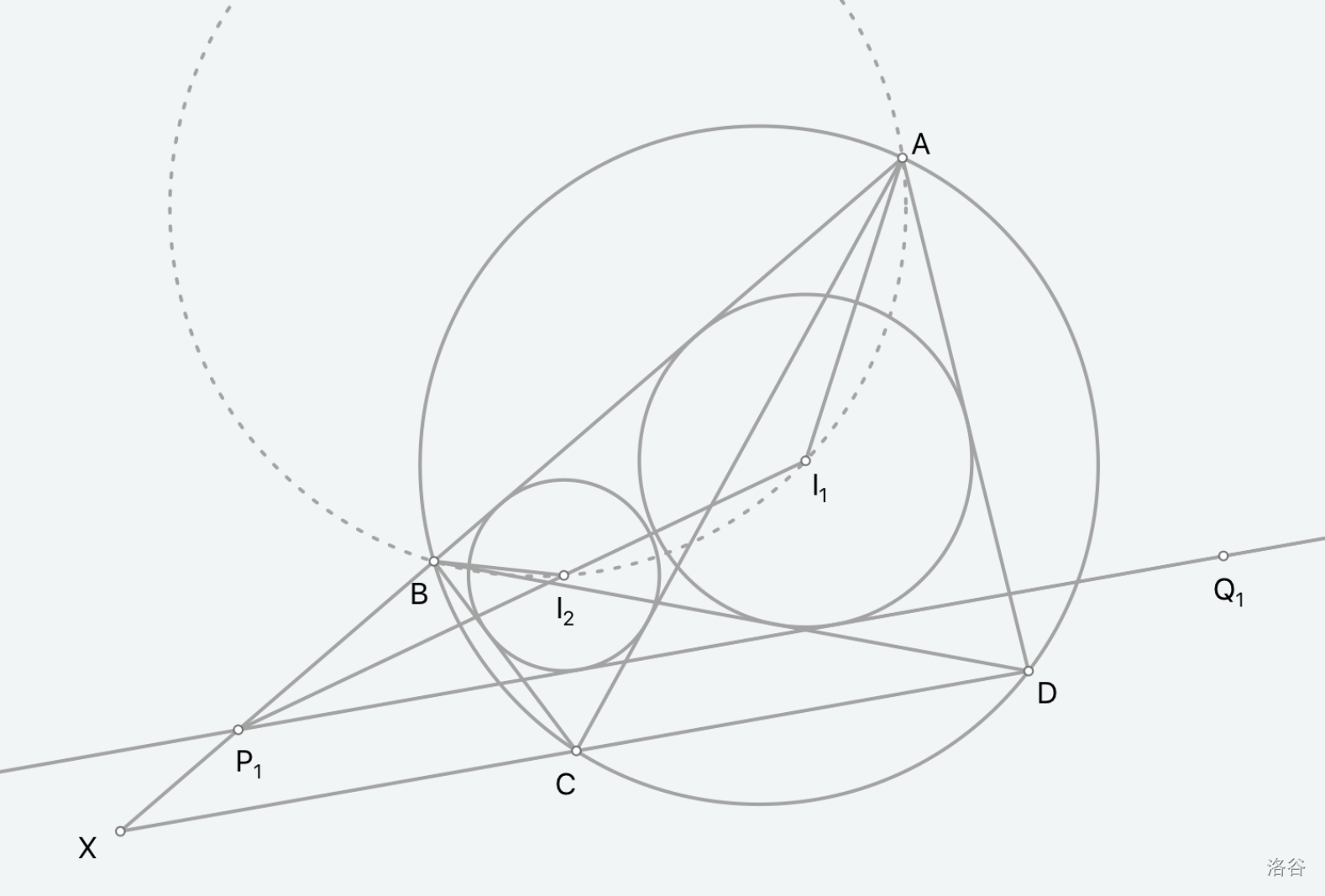
Lemma 1:lAB//CD,其他同理.
Proof:作 AB,IAIB,lAB 交点 P,AB,CD 交点 X.
$\because \angle AI_AB=\dfrac{\pi+\angle ADB}{2}=\dfrac{\pi+\angle ACB}{2}=\angle AI_BB, \therefore A, B, I_B, I_A$ 四点共圆.
$\therefore \angle API_A=\angle ABI_B-\angle BAI_A=\dfrac{1}{2}\angle ABC-\dfrac{1}{2}\angle BAD=\dfrac{1}{2}\angle AXD,\angle APQ=2\angle API_A=\angle AXD$,即 PQ//CD.
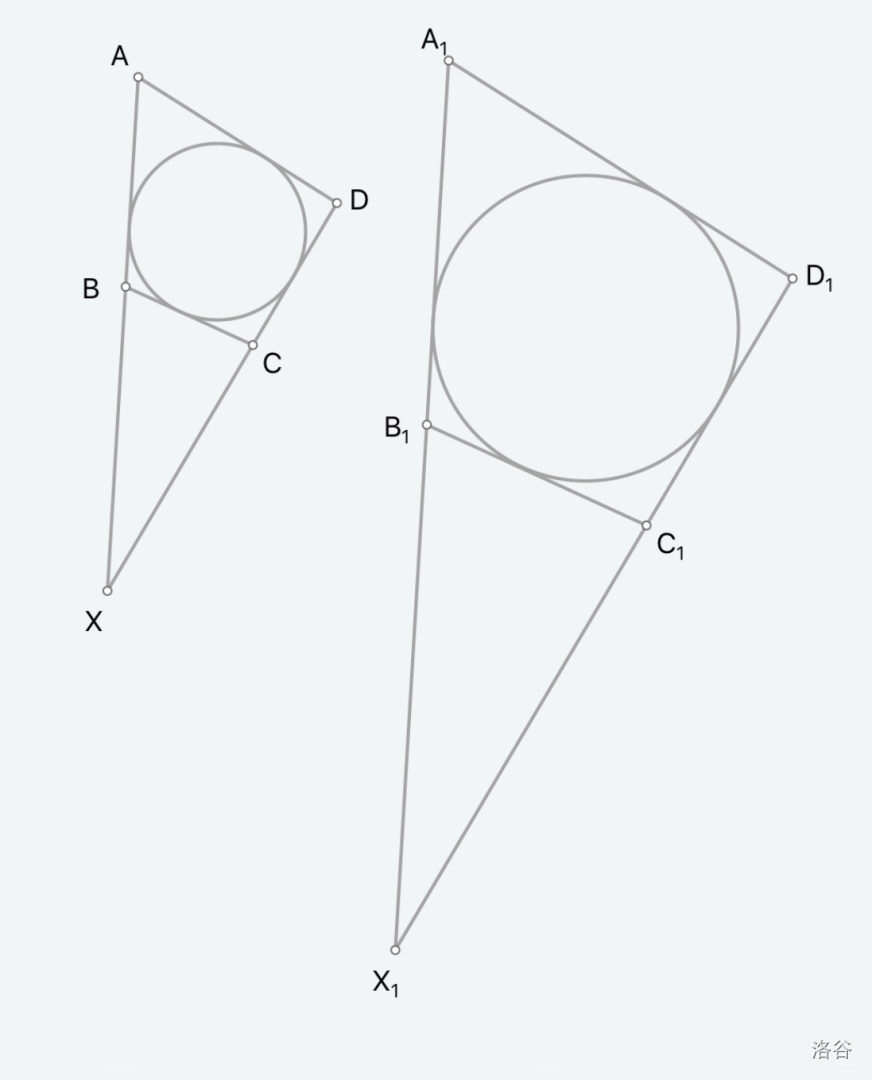
Lemma 2:对应边平行的圆外切四边形相似.
Proof:作 AB,CD 交点 X,A1B1,C1D1 交点 X1.
显然 $\triangle AXD\sim\triangle A_1X_1D_1,\triangle BXCsim\triangle B_1X_1C_1$,设相似比分别为 r,s.
$\because AX+DX-AD=BX+CX+BC,A_1X_1+D_1X_1-A_1D_1=B_1X_1+C_1X_1+B_1C_1, \therefore r(AX+DX-AD)=s(BX+CX+BC)$,即 r=s. 引理得证.
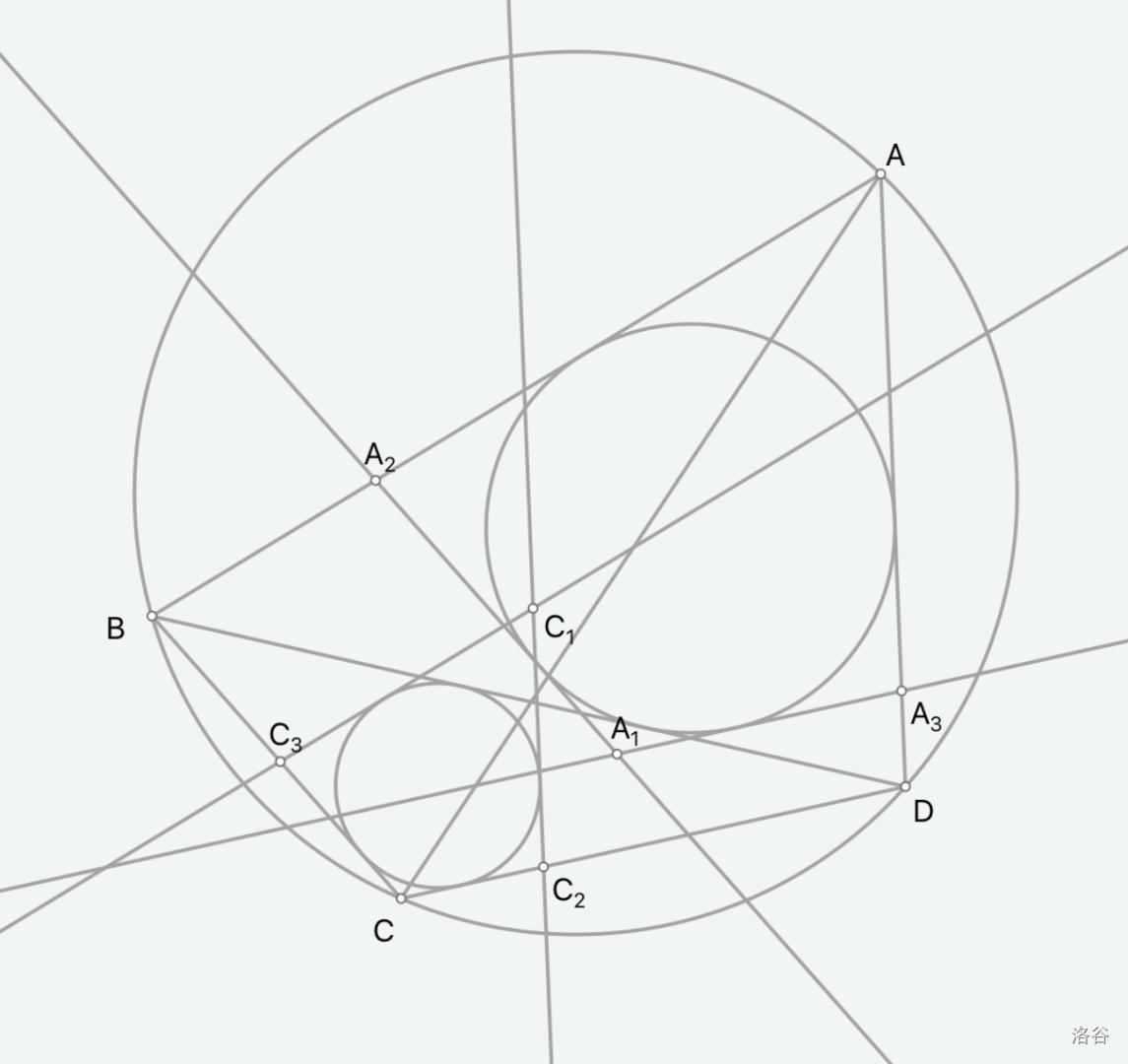
设 $l_{AD}\cap AB=A'',I_{AB}\cap AD=A''',l_{CD}\cap CB=C''',I_{CB}\cap CD=C''$,由 Lemma 1,四边形 AA′′A′A′′′ 与四边形 C′C′′′CC′′ 对应边平行. 由于其都有内切圆,由 Lemma 2,AA′′A′A′′′∼C′C′′′CC′′。 所以 AA′//CC′.
Problem 2
rad. enthusiast
(a) 不存在. 如果存在这样的序列 a,设一个合法的 k 为 k(j),特别地,对于偶数 j,k(j)=j.
如果存在一个 j,使得 k+∞(j) 不存在,那么设 ji=ki(j),i=0,1,⋯,则有 j0<j1<⋯ 且 $\dfrac{a_{j_0}}{j_0}\le \dfrac{a_{j_{i+1}}}{j_{i+1}}$,即 aji+1>j0aj0ji+1,于是 a 不可能有上界,矛盾.
所以对于所有 j=2s−1,k+∞(j) 都存在且为偶数(设为 2t),此时有 2s−1a2s−1≤2ta2t,$\dfrac{a_{2t+1}}{a_{2s-1}}>\dfrac{a_{2t}}{a_{2s-1}}\ge \dfrac{2t}{2s-1}\ge \dfrac{2t}{2t-1}\cdot\dfrac{2t-2}{2t-3}\cdot\cdots\cdot\dfrac{2s}{2s-1}$.
构造一个数列 j0=1,ji+1=k+∞(ji)+1,那么有 $\dfrac{a_{j_{i+1}}}{a_{j_i}}>\dfrac{j_{i+1}-1}{j_{i+1}-2}\cdot\dfrac{j_{i+1}-3}{j_{i+1}-4}\cdot\cdots\cdot\dfrac{j_i+1}{j_i}$.
两边遍历 i=0,1,...,m 相乘,有 $a_{j_{m+1}}=\dfrac{a_{j_{m+1}}}{a_1}\ge\dfrac{2}{1}\cdots\dfrac{4}{3}\cdot\cdots\cdot\dfrac{j_{m+1}-1}{j_{m+1}-2}$.
令 m→+∞,左边有界,右边发散[1],矛盾. 所以不存在这样的序列 a.
(b) 存在,构造 f1=1,fi+1=i2i2+1fi, an=f⌈n⌉,则如果 n=m2,那么 $\dfrac{a_{n^2}}{n^2}=\dfrac{f_n}{n^2}=\dfrac{f_{n+1}}{n^2+1}=\dfrac{a_{n^2+1}}{n^2+1}$. 并且 fi 收敛[2],所以 ai 有界.
[1] xn=i=1∏n2i−12i 发散.
证明:$x_n^2=\prod\limits_{i=1}^n\dfrac{2i}{2i-1}\prod\limits_{i=1}^n\dfrac{2i}{2i-1}=2\prod\limits_{i=2}^n\dfrac{2i}{2i-1}\prod\limits_{i=1}^n\dfrac{2i}{2i-1}\ge 2\prod\limits_{i=2}^n\dfrac{2i-1}{2i-2}\prod\limits_{i=1}^n\dfrac{2i}{2i-1}=4n+2$.
所以 xn 发散.
[2] yn=i=1∏ni2i2+1 收敛.
证明:$y_n=2\prod\limits_{i=2}^n\dfrac{i^2+1}{i^2}\le 2\prod\limits_{i=2}^n\dfrac{i^2}{i^2-1}=2\prod\limits_{i=1}^n\dfrac{i^2}{(i+1)(i-1)}=4m/(m+1)=4-4/(m+1)<4$.
所以 yn 收敛.
Problem 3
a3
若 n 是素数,不妨设对应的 k 为 k(j),f(j) 满足 f(j)≡j+k(j),1≤f(j)≤n.
构造一个有向图 G=(V,E),V={1,2,...,n},E={(j,f(j)):j∈V}. 则 G 是有向基环森林. G 中必有一个环 v1v2⋯vt(2≤t≤n).
设 #{s∈{1,2,⋯,t}:vs>vs+1}=p,则 $n\mid\sum\limits_{s=1}^t\sum\limits_{i=0}^{v_{s+1}-v_{s}-1}a_{v_s+i}=p\sum\limits_{i=1}^na_i$.
因为 1≤p<t≤n,所以 (n,p)=1,于是 n∣i=1∑nai,矛盾.
若 n 是合数,取 m∣n,1<m<n,a1=a2=⋯=an−1=m,an=n 即可.
Problem 4
a3
令 n=1,则 f(n)=1,f(f(n))=1. 下设 n≥2,此时 f(n) 显然不为 1(否则令 m←n−1,矛盾).
下面的 x∈N≥2∗,k∈N∗.
设 g(n) 为满足 n∣f(x) 的最小 x(一定存在,因为 f(2),f(3),...,f(f(n)+1) 中必有一个是 n 的倍数).
通过归纳法可以证明:n∣f(x)⟺x≡g(n)(modf(n)) [1].
在 [1] 中令 n←kn,则有 $x\equiv g(kn)\pmod{f(kn)}\iff kn\mid f(x)\Rightarrow n\mid f(x)\iff x\equiv g(n)\pmod{f(n)}$. 所以 f(n)∣f(kn) [2].
在 [1] 中令 n←f(n),x←kn,则有 f(n)∣f(kn)⟺kn≡g(f(n))(modf(f(n))),即 kn≡g(f(n))(modf(f(n))). 再令 k←k+1,有 kn≡(k+1)n(modf(f(n))),所以 f(f(n))∣n,g(f(n))≡0(modf(f(n))) [3].
在 [1] 中令 x←f(n),有 n∣f(f(n))⟺f(n)≡g(n)(modf(n)),即 n=f(f(n))⟺g(n)≡0(modf(n)) [4].
在 [4] 中令 n←f(n),有 f(n)=f(f(f(n)))⟺g(f(n))≡0(modf(f(n))). 结合 [3] 知 f(n)=f(f(f(n))) [5].
在 [1] 中令 n←f(f(n)),有 $f(f(n))\mid f(x)\iff x\equiv g(f(f(n)))\pmod{f(f(f(n)))}$. 结合 [3], [5] 知 f(f(n))∣f(x)⟺x≡0(modf(n)).
由于 f(f(n))∣n,所以 f(f(n))∣x⇐n∣x,$x\equiv0\pmod{f(n)}\Leftarrow x\equiv g(n)\pmod{f(n)}$. 所以 g(n)≡0(modf(n)),即 n=f(f(n))(由 [4]).




