#194. 「一本通 5.6 练习 5」锯木厂选址
「一本通 5.6 练习 5」锯木厂选址
题目描述
原题来自:CEOI 2004
从山顶上到山底下沿着一条直线种植了 棵老树。当地的政府决定把他们砍下来。为了不浪费任何一棵木材,树被砍倒后要运送到锯木厂。
木材只能朝山下运。山脚下有一个锯木厂。另外两个锯木厂将新修建在山路上。你必须决定在哪里修建这两个锯木厂,使得运输的费用总和最小。假定运输每公斤木材每米需要一分钱。
你的任务是编写一个程序,读入树的个数和他们的重量与位置,计算最小运输费用。
输入格式
输入的第一行为一个正整数 ,表示树的个数 。树从山顶到山脚按照 标号。
接下来 行,每行有两个整数 和 。分别表示第 棵树的重量(公斤为单位)和第 棵树和第 棵树之间的距离。最后一个数 ,表示第 棵树到山脚的锯木厂的距离。
输出格式
输出仅一个数,表示最小的运输费用。
样例
9
1 2
2 1
3 3
1 1
3 2
1 6
2 1
1 2
1 1
26
下图展示了对于样例输入的最佳伐木场设置位置,树木用一个圆表示,伐木场用黑色标出。结果为:
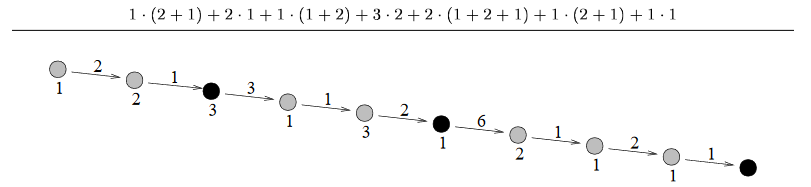
数据范围与提示
对于 分的数据,$2\le n\le 2\times 10^4,1\le w_i\le 10^4,0\le d_i\le 10^4$,保证所有树运到山脚的锯木厂所需要的费用小于 分。(本部分数据为原数据)
对于另外 分的数据,,保证所有计算均可在 位有符号整数下进行。
