#P9431. [NAPC-#1] Stage3 - Jump Refreshers
[NAPC-#1] Stage3 - Jump Refreshers
题目背景
题目描述
注意本题中 kid 的移动方式与 iw 游戏中不同()。
kid 面前有一个无穷大的竖直二维平面。坐标系 轴正方向为从左到右, 轴正方向为从下到上。
地图(该平面)内有 个位置互不相同的可以无限重复使用的跳跃球。当 kid 正好位于某跳跃球位置时,他可以让 shift 键按下,然后他会瞬间上升 格(此期间不能左右移动)。他每秒往下坠落 格,同时每秒 kid 可以选择:向左或向右移动 1 格,或者不移动。当 kid 不在跳跃球上时他不能起跳。
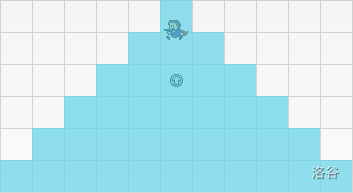
上图是一个例子,蓝色区域表示 kid 在跳跃球(箭头)处起跳()后可以达到的区域。kid 每秒时的横纵坐标只能是整数,即:我们认为他不能达到非整点位置。
现在,kid 把存档放在了第 个跳跃球处(即起点是第 个跳跃球处;此时可以立即起跳)。定义 kid 的得分为他经过(即在某处起跳:显然起跳之后可以回到原位置)的不同跳跃球的个数。kid 想知道他可以最多获得多少得分(不需要(但可以)回到起点),请你告诉他吧。
再次提醒:跳跃球可以无限重复使用,即 kid 可以在某个跳跃球上无限起跳。
输入格式
本题单测试点内有多组数据。
第一行仅两个整数 表示测试数据的数量和测试点编号。特别地,样例的 。
对于每组测试数据:
第一行三个正整数 含义如上所述。
后 行每行两个正整数 表示第 个跳跃球的位置。
输出格式
对于每组测试数据输出一行一个正整数表示最大得分。
4 0
4 2 1
2 4
1 1
5 2
4 1
5 3 4
1 7
2 4
3 2
4 5
8 2
4 1 2
1 1
1 2
1 3
4 1
4 2 1
1 1
4 1
1 4
4 4
3
4
4
1
提示
【数据范围】
本题采用捆绑测试。
$$\def\r{\cr\hline} \def\None{\text{None}} \def\arraystretch{1.5} \begin{array}{c|c|c|c} \textbf{Subtask} & id= & \textbf{Sp. Constraints} & \textbf{Score}\r \textsf1& 1\sim3,36 & n\leqslant10,T\leqslant10 & 10 \r \textsf2& 4\sim7 & \sum n\leqslant200 & 15 \r \textsf3& 8\sim13 & \mathbf A & 25 \r \textsf4& 14\sim18 & \mathbf B & 10 \r \textsf5& 19\sim35 & - & 40 \r \end{array} $$其中 表示单测试点内所有 的总和。
表示 。
- 特殊性质 :保证对于任意不同跳跃球 ,如果 kid 理论上能从 跳到 (理论上:不考虑 kid 能否从起点到达 的问题,下同),那么他理论上一定不可以从 跳到 。
- 特殊性质 :保证对于任意跳跃球 ,如果 kid 理论上能从 跳到 ,那么他理论上一定可以从 跳到 。
注意上面的“从 跳到 "不一定非得一跳到位。比如样例 #1-2 中可以从第 个跳到第 个:。
对于 的数据,,,,,,, 互不相同。
【样例解释 #1-1】
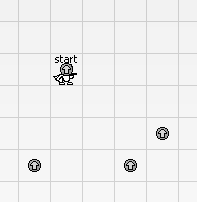
,容易发现离开初始位置就上不去了。所以 kid 要么往左边碰第 个跳跃球,得分为 ;要么往右边跳,经过第 和第 个跳跃球,得分为 。
【样例解释 #1-2】
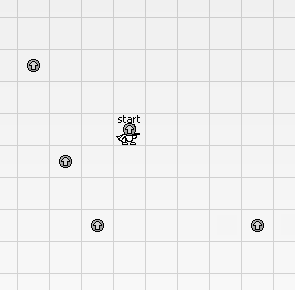
,kid 可以先往下走一圈()跳回起点,然后往右去碰第 个球。左上角的第 个跳跃球是碰不到的。
【样例解释 #1-3】
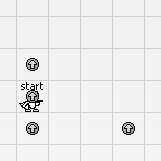
通过最上面那个球是可以跳到右边的。
【样例解释 #1-4】
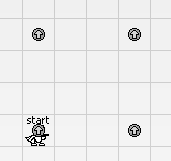
有 的 人 。
Related
In following homework: