题目描述

平面上有 $n$ 个点，第 $i$ 个点坐标为 $(x_i, y_i)$。连接 $i, j$ 两点的边权为 $\sqrt{(x_i - x_j) ^ 2 + (y_i - y_j) ^ 2}$。求最小生成树的边权之和。

输入格式

第一行一个整数 $n$。

接下来 $n$ 行，每行输入两个整数 $x_i, y_i$。

输出格式

输出一行一个实数，表示答案。

当你的答案与标准输出的绝对误差或相对误差在 $10^{-6}$ 内时，就会被视为正确。

4
0 0
1 2
-1 2
0 4

6.472136

提示

样例解释 1

该样例中，最小生成树如下图所示：

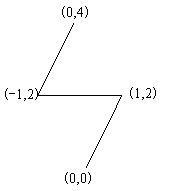
边权之和为 $2 \sqrt{5} + 2 \approx 6.47213595500$。

数据规模与约定

• 对于 $50\%$ 的数据，$n \le 5000$。
• 对于 $100\%$ 的数据，$3 \le n \le 10 ^ 5$，$\lvert x_i \rvert, \lvert y_i \rvert \le 10 ^ 5$。