题目描述
计算满足如下条件的带标号有根树数量:
- 这棵树一共有 n 个节点。
- 每个节点都有一个整数权值,且在区间 [1,m] 内。
- 每个节点的权值都不大于其父节点的权值。
答案可能很大,只需输出答案对 998244353 取模的值。
两棵树 T1 和 T2 不同当且仅当两棵树的节点数不同或者根节点不同或者存在一个编号 i 使得 T1 和 T2 中 i 号节点的父节点编号不同或者 i 号节点的权值不同。
输入格式
一行两个正整数 n,m,意义见题目描述。
输出格式
一行一个整数,所求答案。
2 2
6
4 6
13524
9 34
857311624
提示
样例解释
对于第一组样例,
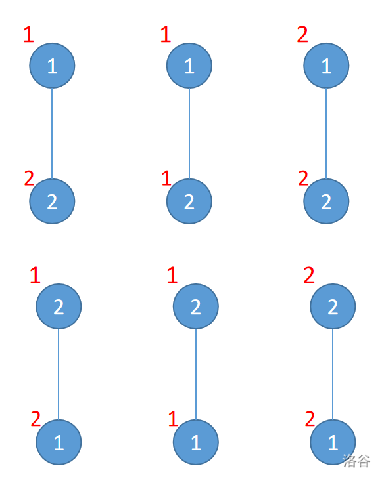
六棵树如上图所示,其中圈内的数字是节点编号,圈外的数字是节点权值。
数据范围
「本题采用捆绑测试」
对于所有测试点,保证 1≤n≤400,1≤m<998244353。
Subtask 1 (7 pts) n=3,m=3。
Subtask 2 (11 pts) m=1。
Subtask 3 (19 pts) n,m≤6。
Subtask 4 (17 pts) n≤7。
Subtask 5 (11 pts) n,m≤50。
Subtask 6 (35 pts) 无特殊限制。

