题目背景

树链剖分，计算机术语，指一种对树进行划分的算法，它先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链，然后再通过数据结构（树状数组、SBT、SPLAY、线段树等）来维护每一条链。(摘自百度百科)

题目描述

大宁最近在研究树链剖分。他发现树链剖分的时间复杂度主要由轻重链的划分方式保证，最常见的剖分方式是按照子树大小剖分。如图（摘自百度百科），黑边为重链，长度任意，白边为轻链，长度全部为1。注意，下图 1-2, 1-3 为不同轻链。

其中对于每个节点，其在重链上的儿子叫做重儿子，且只有唯一一个，而叶子节点没有重儿子。例如对于图上 1 号点，重儿子是 4 号点。显然，对于不同剖分方式，同一组查询访问的链的数量不同。现在给定一棵根为 1 号节点的有根树和若干询问操作，每次询问访问从 $u$ 到 $v$ 上面的所有轻重链一次。例如在上图的剖分方式中，查询 3 到 8 一共访问了 3 条：轻链 1-3，重链 1-4，轻链 4-8；查询 3 到 11 一共访问了 3 条：轻链 1-3，轻链 1-2，重链 2-11。

大宁请你给出一种剖分方案，使所有询问操作总共访问的轻重链总条数最小，由于可能有许多合法方案，请任意输出一种，我们提供Special Judge检验你的方案的正确性。

设你的剖分方式的查询链数为 $x$，std 答案的查询数为 $x_0$，评分参数为 $a$ 。

你得到的分数是：

• $10$ 分 当 $x\leq x_0$ 。

• $8$ 分 当 $0<(x-x_0)\leq a$ 。

• $7$ 分 当 $a<(x-x0)\leq 2\times a$ 。

• $6$ 分 当 $2\times a<(x-x0)\leq 3\times a$ 。

• $1$ 分 输出了合法的方案。

$a=\lfloor\frac{q}{300}\rfloor$, $q$ 为询问总数。

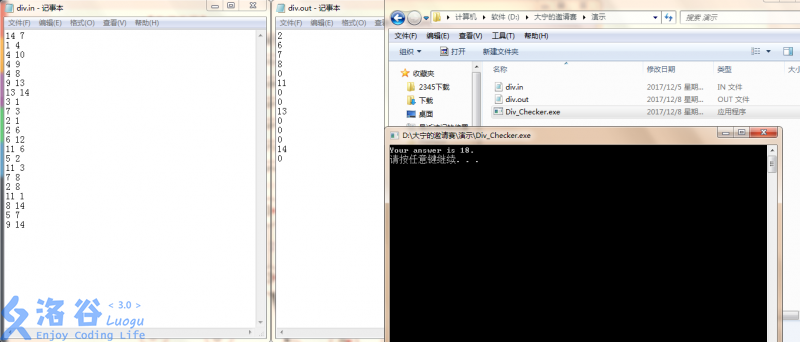
我们提供了 Div\_Checker.exe 来检验你的答案。把它放到 div.in , div.out 同文件夹下运行，其中 div.in 是输入数据的文件形式, div.out 是你的程序在该输入下的输出。如果你的 div.out 答案合法，它会返回：

Your answer is XXX.

XXX 是你的剖分方式在该输入数据下的查询次数，否则返回：

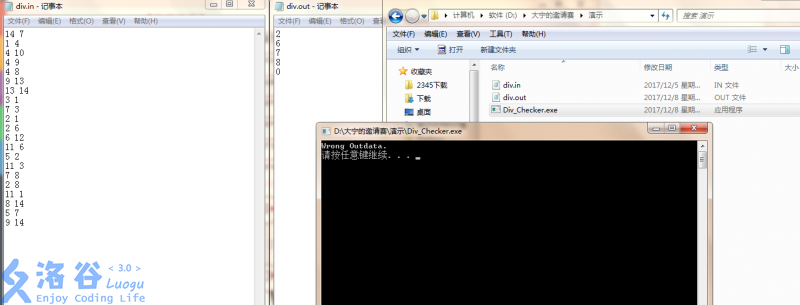
Wrong Outdata.

注意: 在正式提交的时候不能使用文件输入输出。

输入格式

第一行有两个正整数 $n$ 和 $q$ ，表示该树的节点数 $n$ 和查询次数 $q$ 。

接下来 $n-1$ 行，各有两个正整数 $u$ ，$v$ ，表示 $u$ 和 $v$ 之间有一条边。

接下来 $q$ 行为 $q$ 个询问，为 $U$，$V$，表示有一次从 $U$ 到 $V$ 的询问。

输出格式

一共 $n$ 行，对于 $i$ 号节点，如果它不是叶子节点，那么输出它在你的剖分方案里的重儿子，否则输出 0。

14 7
1 4
4 10
4 9
4 8
9 13
13 14
3 1
7 3
2 1
2 6
6 12
11 6
5 2
11 3
7 8
2 8
11 1
8 14
5 7
9 14

2
6
7
8
0
11
0
0
13
0
0
0
14
0

提示

样例即为上图，但图上的剖分方式对于此处的查询并非最优。

对于 $20\%$ 的数据，$n,q<=10$

对于 $60\%$ 的数据，$n,q<=1000$

对于 $100\%$ 的数据，$1<=n<=100000$,$1<=q<=200000$ ,保证给出的是一棵合法的树。

Div_Checker下载

如果对Checker的使用方式不太理解，请参照下面的图片

图中数据为样例。

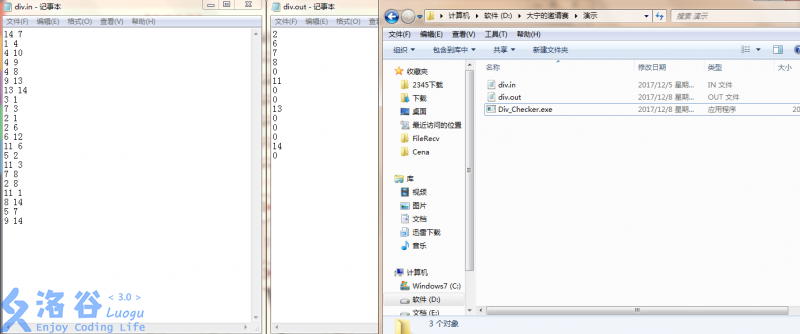
一个合法方案的输出。

不合法方案的输出。

---

$\text{upd 2022.8.26}$：新增加一组 Hack 数据。