题目描述

Publishing maps is not an easy task. First you need some appropriate transformation to display the earth’s spherical shape in a two-dimensional plane. Then another issue arises – most high-quality maps are too large to be printed on a single page of paper. To cope with that, map publishers often split maps into several rectangular tiles, and print each tile on one page. In this problem, you will examine this “tiling” process.

The International Cartographic Publishing Company (ICPC) needs to cut their printing costs by minimizing the number of tiles used for their maps. Even with a fixed tile size (determined by the page size) and map scale, you can still optimize the situation by adjusting the tile grid. The left side of Figure G.1 shows 14 map tiles covering a region. The right side shows how you can cover the same region with only 10 tiles, without changing the tile sizes or orientation.

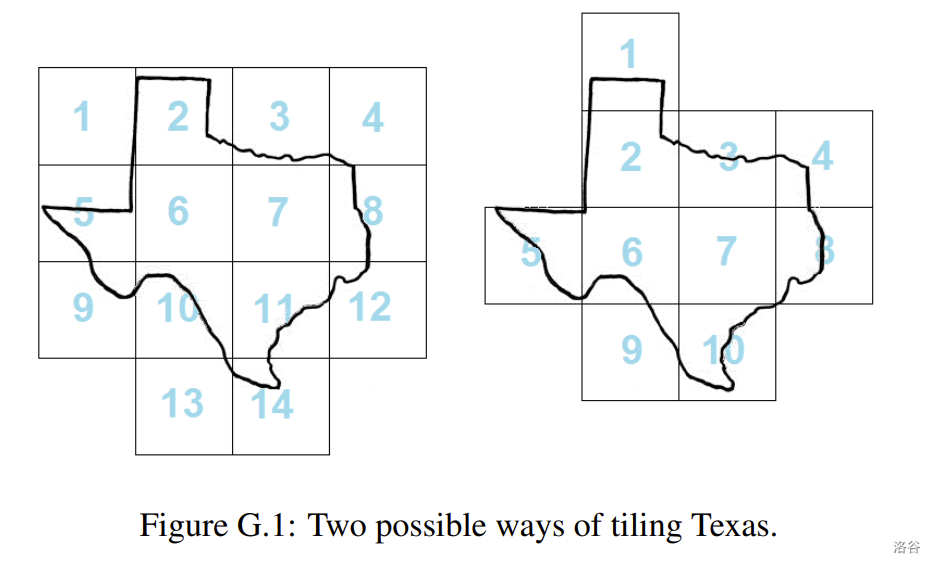
Your task is to help the ICPC find the minimum number of tiles needed to cover a given region. For simplicity, the region will be given as a closed polygon that does not intersect itself.

Note that the tiles must be part of a rectangular grid aligned with the $x$-axis and $y$-axis. That is, they touch each other only with their whole sides and cannot be rotated. Also note that although all input coordinates are integers, tiles may be located at non-integer coordinates.

The polygon may touch the edges of marginal lines (as in Sample Input 2). However, to avoid floatingpoint issues, you may assume the optimal answer will not change even if the polygon is allowed to go outside the map tiles by a distance of $10^{-6}$.

输入格式

The input consists of a single test case. The first line of a test case contains three integers: $n, x_s$, and $y_s$. The number of polygon vertices is $n (3 \leq n \leq 50)$, and $x_s$ and $y_s (1 \leq x_s, y_s \leq 100)$ are the dimensions of each tile. Each of the next $n$ lines contains two integers $x$ and $y (0 \leq x \leq 10x_s, 0 \leq y \leq 10y_s)$, specifying the vertices of the polygon representing the region (in either clockwise or counter-clockwise order).

输出格式

Display the minimal number of tiles necessary to cover the whole interior of the polygon.

题目大意

【题目描述】

出版地图并非易事。首先，你需要进行适当的变换，以在二维平面上显示地球的球形形状。接着出现另一个问题——大多数高质量的地图都太大，无法印在一页纸上。为了解决这个问题，地图出版商通常将地图分割成若干个矩形块，并在每页上打印一个块。在这个问题中，你将研究这种“瓦片化”过程。

国际制图出版公司（ICPC）需要通过最小化用于其地图的瓦片数量来削减印刷成本。即使固定了瓦片大小（由页面大小决定）和地图比例，你仍然可以通过调整瓦片网格来优化情况。图 G.1 的左侧显示了覆盖一个区域的 14 个地图瓦片。右侧显示了如何在不改变瓦片大小或方向的情况下，仅用 10 个瓦片覆盖相同的区域。

你的任务是帮助 ICPC 找出覆盖给定区域所需的最少瓦片数量。为简化起见，该区域将给出为不自相交的闭合多边形。

请注意，瓦片必须是与 $x$ 轴和 $y$ 轴对齐的矩形网格的一部分。也就是说，它们只能用完整的边接触，不能旋转。另外，尽管所有输入坐标都是整数，瓦片的位置可以是非整数坐标。

多边形可能接触边界线的边缘（如样例输入 2 中所示）。但是，为避免浮点数问题，可以假设即使允许多边形超出地图瓦片的距离为 $10^{-6}$，最优答案也不会改变。

【输入格式】

输入包含一个测试用例。测试用例的第一行包含三个整数：$n, x_s$ 和 $y_s$。多边形的顶点数为 $n (3 \leq n \leq 50)$，$x_s$ 和 $y_s (1 \leq x_s, y_s \leq 100)$ 是每个瓦片的尺寸。接下来的 $n$ 行中的每一行包含两个整数 $x$ 和 $y (0 \leq x \leq 10x_s, 0 \leq y \leq 10y_s)$，指定表示区域的多边形的顶点（按顺时针或逆时针顺序）。

【输出格式】

输出覆盖多边形的整个内部所需的最少瓦片数量。

翻译来自于：ChatGPT。

12 9 9
1 8
1 16
6 16
9 29
19 31
23 24
30 23
29 18
20 12
22 8
14 0
14 8

10

4 5 7
10 10
15 10
15 17
10 17

1