高精度计算（Arbitrary-Precision Arithmetic），也被称作大整数（bignum）计算，运用了一些算法结构来支持更大整数间的运算（数字大小超过语言内建整型）。

https://oi-wiki.org/math/bignum/

存储

在平常的实现中，高精度数字利用字符串表示，每一个字符表示数字的一个十进制位。因此可以说，高精度数值计算实际上是一种特别的字符串处理。

读入字符串时，数字最高位在字符串首（下标小的位置）。但是习惯上，下标最小的位置存放的是数字的 ​最低位​，即存储反转的字符串。这么做的原因在于，数字的长度可能发生变化，但我们希望同样权值位始终保持对齐（例如，希望所有的个位都在下标 [0]，所有的十位都在下标 [1]……）；同时，加、减、乘的运算一般都从个位开始进行（回想小学的竖式运算），这都给了「反转存储」以充分的理由。

四则运算

四则运算中难度也各不相同。最简单的是高精度加减法，其次是高精度—单精度（普通的 int）乘法和高精度—高精度乘法，最后是高精度—高精度除法。

我们将按这个顺序分别实现所有要求的功能。

加法

高精度加法，其实就是竖式加法啦。

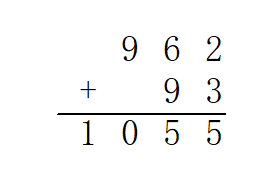
也就是从最低位开始，将两个加数对应位置上的数码相加，并判断是否达到或超过 。如果达到，那么处理进位：将更高一位的结果上增加 ，当前位的结果减少 。

减法

高精度减法，也就是竖式减法啦。

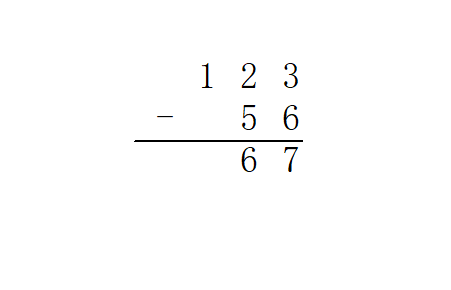
从个位起逐位相减，遇到负的情况则向上一位借 。整体思路与加法完全一致。

乘法

高精度—单精度

高精度乘法，也就是竖……等会儿等会儿！

先考虑一个简单的情况：乘数中的一个是普通的 int 类型。有没有简单的处理方法呢？

一个直观的思路是直接将 每一位上的数字乘以 。从数值上来说，这个方法是正确的，但它并不符合十进制表示法，因此需要将它重新整理成正常的样子。

重整的方式，也是从个位开始逐位向上处理进位。但是这里的进位可能非常大，甚至远大于 ，因为每一位被乘上之后都可能达到 的数量级。所以这里的进位不能再简单地进行 运算，而是要通过除以 的商以及余数计算。详见代码注释，也可以参考下图展示的一个计算高精度数 乘以单精度数 的过程。

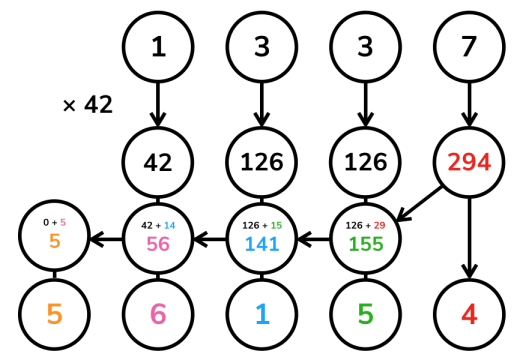
当然，也是出于这个原因，这个方法需要特别关注乘数 的范围。若它和 （或相应整型的取值上界）属于同一数量级，那么需要慎用高精度—单精度乘法。