8 pts for each of P1~P10

20 pts for each of P11~P12

40 pts for each of P13~P14

---

In P1, $E[]$ means the expectation.

In P2 and P7, $\iota=\sqrt{-1}$.

In P5, $e$ refers to the eccentricity of a conic curve.

---

1. $\set{a,b,c}\subseteq\set{1,2,3,4,5,6},a<b<c;E[(a-b)(b-c)]=\_\_\_\_\_\_\_\_.$
2. $z\in\mathbb{C},2025z^{2025}+2024\iota z^{2024}+2024\iota z-2025=0;|z|=\_\_\_\_\_\_\_\_.$
3. $a_1=\dfrac{4}{3},a_{n+1}=a_n^2-a_n+1;\lfloor\sum\limits_{i=1}^{5000}\dfrac{1}{a_i}\rfloor=\_\_\_\_\_\_\_\_.$
4. $\lambda\in\mathbb{R},\forall\triangle ABC,\dfrac{1}{\sin A}+\dfrac{1}{\sin B}\ge\dfrac{\lambda}{3+2\cos C};\lambda\in\_\_\_\_\_\_\_\_.$
5. $l$ 过 $\mathcal{C}:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 的焦点 $F(1,0)$，交 $\mathcal{C}$ 于点 $A,B$；若 $OA^2+OB^2<AB^2$ 恒成立，则 $e_{\mathcal{C}}\in\_\_\_\_\_\_\_\_.$
6. $a,b,c\ge0,a+b+c=1; (\sqrt{4a+1}+ \sqrt{4b+1}+\sqrt{4c+1})_{\min}=\_\_\_\_\_\_\_\_.$
7. $z\in\mathbb{C},|z|=1;|z^2+\iota z^2+1|\in\_\_\_\_\_\_\_\_.$
8. 在 $\triangle ABC$ 中，$\angle A=\dfrac{\pi}{2}$，$\bigodot O$ 与 $AB,AC$，圆心 $O$ 在 $BC$ 上，$\triangle ABC$ 周长为 $152$，$\bigodot O$ 的半价为 $19$；$\triangle ABC$ 的面积为 $\_\_\_\_\_\_\_\_.$
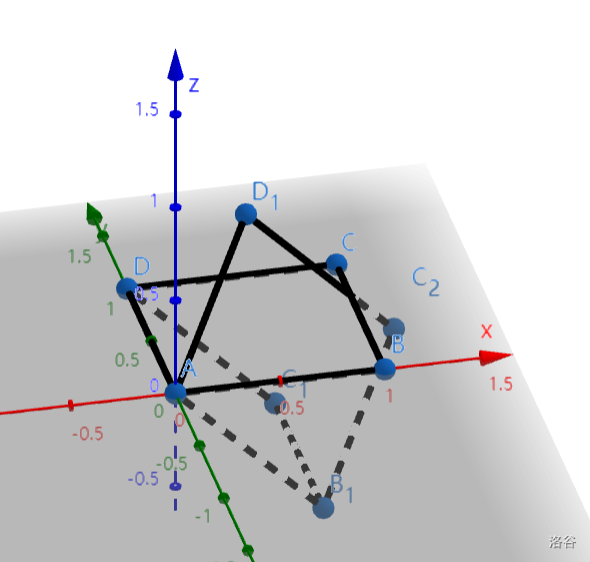
9. $A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0)$，四边形 $ABCD$ 绕轴 $AD$ 旋转 $\theta(\theta\in(0,\dfrac{\pi}{2}))$ 得到 $AB_1C_1D$，再绕轴 $AB_1$ 旋转 $\theta$ 得到 $AB_1C_2D_1$；如果 $z_{D_1}>0$，则 $C_2=\_\_\_\_\_\_\_\_.$ （用 $\theta$ 表示）
10. $q=\dfrac{a}{b}\in\mathbb{Q},a,b\in\mathbb{Z}_+,b\le10; \sum_{|[\sqrt{q},q)\cap\mathbb{Z}|=19}q=\_\_\_\_\_\_\_\_.$
11. $a_k=\sum\limits_{i=k^2}^{k^2+2k}\dfrac{1}{i}$；求 $\sum\limits_{k=1}^n(\lfloor\dfrac{1}{a_k}\rfloor+\lfloor\dfrac{1}{a_k}+\dfrac{1}{2}\rfloor).$
12. 直线 $l_1$ 与抛物线 $y=ax^2+bx+c(a\ne0)$ 交于点 $A,B$，直线 $l_2//l_1$，与 $y=ax^2+bx+c$ 切于点 $D$；证明：三角形 $ABD$ 的面积比上弓形 $ABD$ 的面积为定值.
13. $A$ 在三角形 $BCD$ 内部，$E$ 在射线 $DB$ 上，$AE=CE$，$\angle ECD=\angle CAB$，$F$ 在线段 $CD$ 上，且 $A,B,D,F$ 四点共圆；证明： $BF=BC$.
14. 求所有正整数序列 $\set{a_n}_{n=1}^{\infty}$，使得 $\forall n\ge3:\sum\limits_{i=1}^{n-2}\dfrac{1}{a_ia_{i+2}}=1-\dfrac{1}{\sum\limits_{i=1}^{n-1}a_i^2}.$

---

Anwser

1. $\dfrac{14}{5}$
2. $1$
3. $2$
4. $8$
5. $(0,\dfrac{\sqrt{5}-1}{2})$
6. $2+\sqrt{5}$
7. $[\sqrt{2}-1,\sqrt{2}+1]$
8. $\dfrac{5776}{7}$
9. $(\cos\theta-\sin^2\theta,\cos\theta,\sin\theta+\sin\theta\cos\theta)$ 或 $(\cos\theta+\sin^2\theta,\cos\theta,\sin\theta\cos\theta-\sin\theta)$
10. $\dfrac{1505}{2}$

---

直接算即可。

$S=\sum\limits_{a<b<c}(a-b)(b-c)=\sum\limits_{b=1}^6\sum\limits_{a=1}^{b-1}\sum\limits_{c=b+1}^6(a-b)(b-c)=\sum\limits_{b=1}^6\dfrac{b(b-1)}{2}\cdot\dfrac{(6-b)(6-b-1)}{2}=56$。

$E=\dfrac{S}{C_6^3}=\dfrac{14}{5}$。

老题，可以直接写答案为 $1$。

$2025z^{2025}+2024\iota z^{2024}=2025-2024\iota z$

$|z|^{2024}|2025z+2024\iota|=|2025-2024\iota z|$

$|2025z+2024\iota|^2=(2025z+2024\iota)(2025\overline{z}-2024\iota)=2025^2z\overline{z}+2024^2+2024\cdot2025\iota(z-\overline{z})=2025^2|z|^2+2024^2+2024\cdot2025\iota(z-\overline{z})$

$|2025-2024\iota z|^2=(2025-2024\iota z)(2025+2024\iota \overline{z})=2025^2+2024^2z\overline{z}+2024\cdot2025\iota(z-\overline{z})=2025^2+2024^2|z|^2+2024\cdot2025\iota(z-\overline{z})$

当 $|z|>1$ 时，$|2025z+2024\iota|>|2025-2024\iota z|$，$|z|^{2024}|2025z+2024\iota|>|2025-2024\iota z|$；当 $|z|<1$ 时，$|2025z+2024\iota|<|2025-2024\iota z|$，$|z|^{2024}|2025z+2024\iota|<|2025-2024\iota z|$，均矛盾。所以 $|z|=1$。

见过一次就好了

$a_{n+1}-1=a_n(a_n-1)$

$\dfrac{1}{a_n}=\dfrac{1}{a_n-1}-\dfrac{1}{a_{n+1}-1}$

$\sum\limits_{n=1}^{5000}\dfrac{1}{a_n}=\dfrac{1}{a_1-1}-\dfrac{1}{a_{5001}-1}=3-\dfrac{1}{a_{5001}-1}$

因为 $a_4-1=\dfrac{9490}{6561}>1$，所以 $a_{5001}-1>1$，$\lfloor\sum\limits_{n=1}^{5000}\dfrac{1}{a_n}\rfloor=2$。

设 $A=\alpha+\beta,B=\alpha-\beta,C=\pi-2\alpha(0<\beta<\alpha<\dfrac{\pi}{2})$，则

$\lambda\le f(\alpha,\beta)=\dfrac{(3+2\cos C)(\sin A+\sin B)}{\sin A\sin B}$。

$$\begin{aligned} f(\alpha,\beta)&=\dfrac{4(3-2\cos 2\alpha)\sin\alpha\cos\beta}{\cos 2\beta-\cos 2\alpha}\\ &=\dfrac{4(3-2\cos 2\alpha)\sin\alpha}{2\cos\beta-\frac{\cos 2\alpha+1}{\cos\beta}}\\ &\ge\dfrac{4(3-2\cos 2\alpha)\sin\alpha}{1-\cos 2\alpha}\\ &=\dfrac{4(4\sin^2\alpha+1)\sin\alpha}{2\sin^2\alpha}\\ &=2(4\sin\alpha+\dfrac{1}{\sin\alpha})\\ &\ge2\times4=8 \end{aligned}$$

在 $\cos\beta=0,\sin\alpha=\dfrac{1}{2}$ 即 $A=B=\dfrac{\pi}{6},C=\dfrac{2\pi}{3}$ 时取等。

考试的时候直接猜在 $AB\perp Ox$ 时取等即可。

设 $l:x-c=ky$，联立方程，有 $y_A,y_B$ 是 $\dfrac{(ky+c)^2}{a^2}+\dfrac{y^2}{b^2}=1$ 的两根。由韦达定理，$y_A+y_B=-\dfrac{2kc}{k^2+\frac{a^2}{b^2}},y_Ay_B=-\dfrac{b^2}{k^2+\frac{a^2}{b^2}}$。

由 $OA^2+OB^2<AB^2$，知 $\overrightarrow{OA}\cdot\overrightarrow{OB}<0$，即 $x_Ax_B+y_Ay_B<0$，

$(ky_A+c)(ky_B+c)+y_Ay_B<0$

$(k^2+1)y_Ay_B+kc(y_A+y_B)+c^2<0$

$-(k^2+1)b^2-kc\cdot 2kc+c^2(k^2+\dfrac{a^2}{b^2})<0$

$a^2c^2-b^4<b^2(b^2+c^2)k^2$

所以 $a^2c^2-b^4<0$，$a^2c^2-(a^2-c^2)^2<0$

$ac-a^2+c^2<0$，$e^2+e-1<0$，解得 $\dfrac{-1-\sqrt{5}}{2}<e<\dfrac{-1+\sqrt{5}}{2}$。结合 $0<e<1$ 知 $e\in(0,\dfrac{\sqrt{5}-1}{2})$。

显然 $\sqrt{4a+1}$ 是上凸的，取最小值应在 $(0,0,1)$ 处。

先证 $\sqrt{4a+1}+\sqrt{4b+1}\ge1+\sqrt{4a+4b+1}$。

两边平方，消去平方项，由 $\iff \sqrt{(4a+1)(4b+1)}\ge\sqrt{(4a+4b+1)}$，这是显然的。

所以 $\sqrt{4a+1}+\sqrt{4b+1}+\sqrt{4c+1}\ge1+\sqrt{4a+4b+1}+\sqrt{4c+1}\ge2+\sqrt{4a+4b+4c+1}=2+\sqrt{5}$。

应该是打错了吧，感觉 $|z^2+\iota z+1|$ 才是有意义的题。

$|z^2+\iota z^2|=\sqrt{2}$，$\sqrt{2}-1\le|z^2+\iota z^2+1|\le\sqrt{2}+1$。

设 $1'=19$，则 $C_{\triangle ABC}=8',R_{\bigodot O}=1'$。

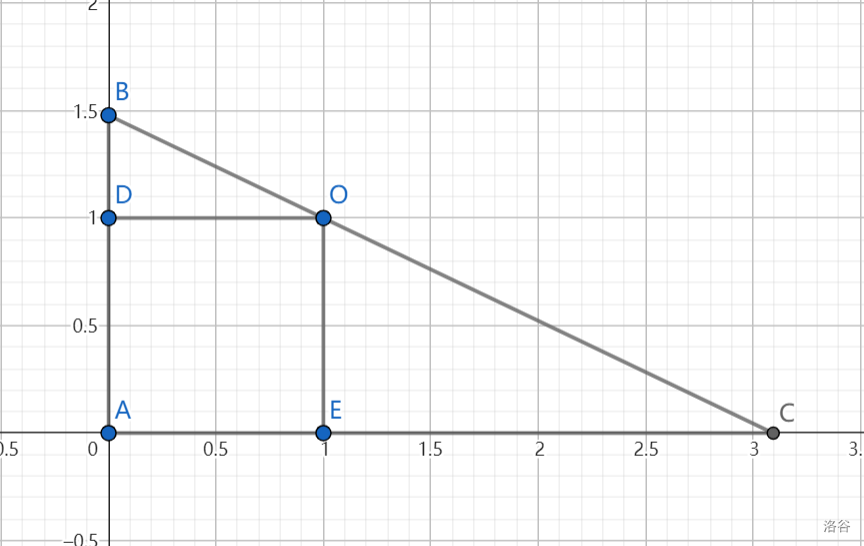
作 $OD\perp AB,OE\perp AC$，设 $BD=k^2\ '(0<k<1,k+\dfrac{1}{k}=t)$，则 $CE=\dfrac{1}{k^2}'$，$OB=\sqrt{k^4+1}'$，$OC=\sqrt{\dfrac{1}{k^4}+1}'=\dfrac{\sqrt{k^4+1}}{k^2}'$，$C_{\triangle ABC}=1'+k^2\ '+1'+\dfrac{1}{k^2}'+\sqrt{k^4+1}'+\dfrac{\sqrt{k^4+1}}{k^2}'=8'$。

所以 $k^2+\dfrac{1}{k^2}+2+\dfrac{(k^2+1)\sqrt{k^4+1}}{k^2}=8$

$t^2+t\sqrt{t^2-2}=8$

$t\sqrt{t^2-2}=8-t^2$

$t^2(t^2-2)=(8-t^2)^2$

$t^2=\dfrac{32}{7}$

$S_{\triangle ABC}=\dfrac{1}{2}(k^2\ '+1')(\dfrac{1}{k^2}'+1')=\dfrac{1}{2}t^2\ ''=\dfrac{1}{2}\times \dfrac{32}{7}\times 19^2=\dfrac{5776}{7}$。

考试时建议跳过（

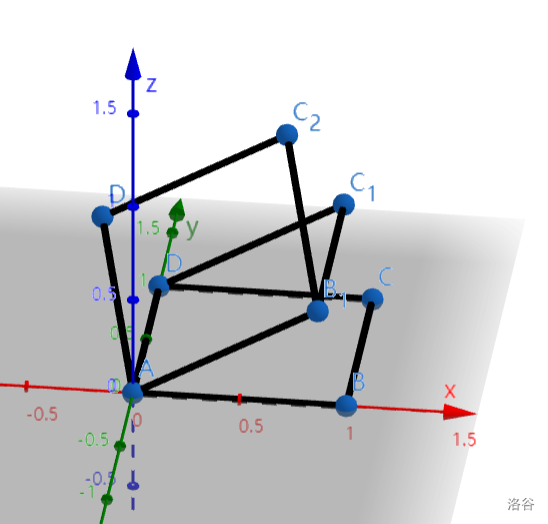
情况 1: $B_1=(\cos\theta,0,\sin\theta),C_1=(\cos\theta,1,\sin\theta)$。

设 $\overrightarrow{B_1C_2}=(x,y,z)$，则 $C_2(x+\cos\theta,y,z+\sin\theta)$。

因为 $\overrightarrow{B_1C_2}\cdot\overrightarrow{B_1C_1}=\cos\theta,\overrightarrow{B_1C_2}\times\overrightarrow{B_1C_1}=\sin\theta\cdot\overrightarrow{B_1A}$，

所以 $y=\cos\theta,(-z,0,x)=(-\sin\theta\cos\theta,0,-\sin^2\theta),C_2=(\cos\theta-\sin^2\theta,\cos\theta,\sin\theta+\sin\theta\cos\theta)$。

情况 2: $B_1=(\cos\theta,0,-\sin\theta),C_1=(\cos\theta,1,-\sin\theta)$。

设 $\overrightarrow{B_1C_2}=(x,y,z)$，则 $C_2(x+\cos\theta,y,z-\sin\theta)$。

因为 $\overrightarrow{B_1C_2}\cdot\overrightarrow{B_1C_1}=\cos\theta,\overrightarrow{B_1C_2}\times\overrightarrow{B_1C_1}=\sin\theta\cdot\overrightarrow{B_1A}$，

所以 $y=\cos\theta,(-z,0,x)=(-\sin\theta\cos\theta,0,\sin^2\theta),C_2=(\cos\theta+\sin^2\theta,\cos\theta,\sin\theta\cos\theta-\sin\theta)$。

$|[\sqrt{q},q)\cap\mathbb{Z}|=19\Rightarrow 23<q\le 24$。

不妨 $a\perp b$。

$b=1$ 时 $q=23+1$，$b=2$ 时 $q=23+\dfrac{1}{2}$。

$b\ge 3$ 时 $2\mid\varphi(b)$，所以 $\sum q=23\varphi(b)+\dfrac{\varphi(b)}{2}$。

所以 $\sum q=23\sum\limits_{b=1}{10}\varphi(b)+1+\dfrac{1}{2}+\dfrac{1}{2}\sum\limits_{b=3}{10}\varphi(b)=23\cdot 32+1+\dfrac{1}{2}+\dfrac{1}{2}\cdot 30=\dfrac{1505}{2}$。

自己补充细节吧。

考试要猜到这个放缩挺难的。

记 $b_k=\lfloor\dfrac{1}{a_k}\rfloor+\lfloor\dfrac{1}{a_k}+\dfrac{1}{2}\rfloor$。

$k=1$ 时 $a_k=\dfrac{11}{6},b_k=0+1=1$。

$k\ge 2$ 时：

$a_k=\sum\limits_{i=k^2}^{k^2+2k}\dfrac{1}{i}>\sum\limits_{i=k^2}^{k^2+2k}(\ln(i+1)-\ln i)=\ln\dfrac{k^2+2k+1}{k^2}>\dfrac{2}{k+1}$；

$a_k=\sum\limits_{i=k^2}^{k^2+2k}\dfrac{1}{i}<\sum\limits_{i=k^2}^{k^2+2k}(\ln(i)-\ln (i-1))=\ln\dfrac{k^2+2k}{k^2-1}<\dfrac{2}{k}$

$b_k=\lfloor\dfrac{1}{a_k}\rfloor+\lfloor\dfrac{1}{a_k}+\dfrac{1}{2}\rfloor=k$。

$\sum\limits_{k=1}^nb_k=\dfrac{n(n+1)}{2}$。

经过平移变换和翻转变换后，不妨设抛物线为 $y=ax^2(a>0)$，$D(x_0,ax_0^2),A(x_1,ax_1^2),B(x_2,ax_2^2)(x_1<x_2)$

则 $2x_0=x_1+x_2$，设 $d=x_0-x_1=x_2-x_0$。

三角形 $ABD$ 的面积为 $a(x_2-x_1)(x_2-x_0)(x_0-x_1)=ad^3$。

弓形 $ABD$ 的面积为 $\dfrac{1}{2}(ax_1^2+ax_2^2)(x_2-x_1)-\int_{x_1}^{x_2}adx^2\operatorname{d}x=\dfrac{4}{3}ad^3$。

故面积比为定值 $\dfrac{3}{4}$。

$BC=BF\iff\angle BCF=\angle BFC\iff\angle BCD=\pi-\angle BFD\iff\angle BCD=\pi-\angle BAD$。这一步很自然地可以想到对称。

作 $A$ 关于 $BD$ 的对称点 $A'$，则 $BC=BF\iff\angle BCD=\pi-\angle BA'D\iff A',B,C,D$ 四点共圆。

设 $BD$ 交以 $E$ 为圆心，$EC$ 为半径的圆于 $X,Y$，交 $CA$ 于 $S$，交 $CA'$ 于 $T$。

因为 $XAYA'$ 为调和四边形，所以 $X,T,Y,S$ 构成调和点列，所以 $ES\cdot ET=EC^2$，$\triangle ESC\sim\triangle ECT$，$\angle ESC=\angle ECT$。

因为 $\angle A'CD=\angle ECD-\angle A'CE=\angle ECD-\angle ECT$，

$\angle A'BD=\angle ABD=\angle CAB-\angle ESC$。

所以 $\angle A'CD=\angle A'BD$，即 $A',B,C,D$ 四点共圆。

根据 $a_3$ 的递推式，直觉上 $a_1,a_2$ 不可能太大，试出来的 $a_n$ 为斐波那契数列。

由题意知 $a_3=\dfrac{a_1^2+a_2^2}{a_1(a_1^2+a_2^2-1)}$，所以 $a_1^2+a_2^2\ge a_1(a_1^2+a_2^2-1)$，$a_1\ge (a_1-1)(a_1^2+a_2^2)\ge2(a_1-1)$，$a_1\le 2$。

如果 $a_1=1$，那么 $a_3=1+\dfrac{1}{a_2^2}$，$a_2=1$，归纳有 $a_n$ 为斐波那契数列。

如果 $a_1=2$，那么 $a_3=\dfrac{4+a_2^2}{6+2a_2^2}<1$ 矛盾。

综上，$a_n$ 为斐波那契数列。